Über den Energieaustausch und die Effektivität des Regenerators
in der Stirlingmaschine in bezug auf das Volumenverhältnis Vmax / Vmin
und die Art des Arbeitsfluids.
Dipl.-Ing. Peter Fette
Am Schäferloch 16,
D-75045 Walzbachtal / Germany
ABSTRAKT:
Achtung: Einige Browser geben anstelle der Symbole mit griechischen Buchstaben lateinische Buchstaben wieder !
In der 2-mal doppelt wirkenden Stirlingmaschine, die auf der 6. International Stirling Engine Conference (6th ISEC) im Mai 1993 in Eindhoven vorgestellt wurde, können relativ hohe Volumenverhältnisse Vmax/Vmin realisiert werden ; |1| Report No. ISEC - 93003. Je höher das Volumenverhältnis in der Maschine um so höher ist auch die pro Umdrehung verrichtete Nutzarbeit des Arbeitsprozesses, vorausgesetzt die Wärmezufuhr- und die Kühlungseinrichtungen können die entsprechend höheren Energieströme bewältigen.
Die vorliegende theoretische Arbeit befasst sich mit der Korrelation der Wirksamkeit des Regenerators, dem Volumenverhältnis Vmax/Vmin und der Charakteristik des Arbeitsfluids in bezug auf den Adiabatenexponent k = Cp / Cv Es kann gezeigt werden, dass der Wirkungsgrad des Regenerators unter bestimmten Bedingungen zugunsten eines geringeren Druckverlustes verringert werden kann. Für sehr hohe Volumenverhältnisse, niedriges Temperaturverhältnis TE/TC und Helium als Arbeitsgas genügt u.U. ein Rohr als Regenerator. Diese Aussagen werden formelmässig abgeleitet; mit den Formeln berechnete Diagramme illustrieren diese Aussagen. Alle Diagramme, Tabellen und Berechnungen sind mit dem Computerprogram STMOT2: gemacht. Die Berechnungsgrundlagen dieses Programms sind in |7| beschrieben.
Nonenclature:
Der Bericht von T. Finkelstein |2| gab den Anlass, für die in |1| beschriebene Maschine ähnliche theoretische Untersuchungen zu machen; speziell in Hinblick auf den Regenerator. Da diese Arbeit speziell für die in |1| beschriebene Maschine gemacht wurde, sind die hier präsentierten Ergebnisse nicht in allen Konsequenzen auch auf andere Stirlingmaschinen übertragbar.
Die in |1| vorgestellte Maschine ist vom a - Typ und ist speziell für die Nutzung von Niedertemperaturwärme konstruiert. Die Wärmeübertragung geschieht durch Beregnung des Arbeitsfluids mit einer Arbeitsflüssigkeit jeweils in den Zylindern, sodass nahezu isotherme Zustandsänderungen realisiert werden können. Einen Heizer oder Kühler wie in herkömmlichen Stirlingmaschinen vom a- Typ gibt es hier nicht. Die Arbeitsflüssigkeit wird ausserhalb der Maschine beheizt bzw. gekühlt. Durch Variation der Arbeitsflüssigkeitsmenge in den Zylindern kann das Volumenverhältnis auf einfache Weise verändert werden. Nicht zuletzt aus diesem Grund ist diese Maschine eine ideale Testmaschine. Aus verschiedenen Gründen kann der Regenerator hier nicht in der üblichen Weise konstruiert sein. Z.B. wird ein herkömmlicher Regenerator in dieser Maschine, die auch mit "compound fluid" also einem Gemisch aus Gas und Dampf arbeiten kann, für die Dampfkomponente unwirksam sein und noch zusätzliche Nachteile haben wie einen unnötigen Druckverlust wegen Tröpfchenbildung.
Grundsätzlich wird ein Regeneratorwärmeaustausch immer verlustbehaftet sein. Man kann aber die Frage aufwerfen, welcher Regeneratorverlust noch tragbar ist und welche anderen Massnahmen neben einem optimalen Regenerator ergriffen werden können, um den thermischen Wirkungsgrad der Maschine zu steigern. Auf diesem Gebiet sind viele theoretische Arbeiten gemacht worden, siehe auch |3|. Mit dieser Untersuchung soll der Versuch gemacht werden, die Probleme aus einem anderen Blickwinkel zu sehen, natürlich immer mit Bezug auf diese spezielle Maschine, die definitionsgemäss mit niedertemperierten Wärmequellen arbeiten soll, und bei der eine nahezu isotherme Wärmeübertragung innerhalb ihrer Arbeitszylinder erfolgt.
Ausgehend von dem idealen isothermen Stirling Prozess sei ein Prozess definiert, bei dem die Zustandsänderungen ebenso verlaufen wie bei diesem, der aber einen verlustbehafteten Regenerator besitzt. Ein solcher Prozess sei ein "de-idealisierter" Prozess genannt. Siehe auch |5|.
Der thermische Wirkungsgrad eines Kraftprozesses ist definiert als das Verhältnis von Nutzarbeit "W" und der dem Prozess zuzuführenden thermischen Energie Qext.
(1) ![]()
Berücksichtigt man alle Phasen des idealen Prozesses dann ist der Wirkungsgrad:
(2) 
Im idealen Stirling Prozess wird unterstellt, dass der Regenerator 100 % wirkt, hreg = 1 . Dann sind die beiden im Regenerator isochorisch auszutauschenden Energiemengen Q2 - 3 (vom Regenerator abzugeben beim konstanten Volumen Vmin ) und Q4 - 1 (bei Vmax vom Regenerator aufzunehmen) einander äquivalent. Daraus folgt: Q2 - 3 + Q4 - 1 = 0. Die extern zuzuführende Energiemenge ist dann für den idealen Prozess allein Qext = Q3 - 4 . Dann ist der ideale Wirkungsgrad:
(3) 
Man stelle sich jetzt den "de-idealisierten" Prozess vor, der mit einem verlustbehafteten Regenerator arbeitet h reg < 1 . Wir definieren einen Verlustfaktor des Regenerators RV = 1 - h reg .
Weiter stelle man sich vor, dass die Nutzarbeit des Prozesses pro Umdrehung "W" die gleiche sein soll wie beim idealen Prozess. Dann muss, für den Fall h reg < 1 , zusätzlich Energie zugeführt werden, damit das Arbeitsfluid am Ende der isochoren Zustandsänderung bei Vmin und vor Beginn der isothermen Expansion die Temperatur "TE" erreicht. Nach der Expansion und dem dann folgenden isochoren Energieentzug bei Vmax muss zusätzliche Energie abgeführt werden, damit das Arbeitsfluid vor Beginn der isothermen Kompression die Temperatur "TC" erhält. Die Energie, die der Regenerator wegen seiner Verluste nicht mehr aufnehmen bzw. abgeben kann ist Qreg = RV * Q2 - 3
Mit diesen Überlegungen definieren wir nun den thermischen Wirkungsgrad des "de-idealisierten" Prozesses zu:
(4) 
Die einzelnen Energiekomponenten Q n - m dieser Gleichung (4) werden nun bestimmt.
Q3 - 4 für die isotherme Expansion:
(5) 
Q1- 2 für die isotherme Kompresssion:
(6) 

Die bei Vmin isochor zuzuführende Energie ist:
(7) ![]()
für h therm bekommen wir nun:
(8) 
Mit den weiteren Vereinfachungen :
Carnot Wirkungsgrad h C = ( TE - TC) / TE ,lässt sich h therm nun in der für Computerberechnungen allgemein geeigneten Form schreiben:
(9) 
Zur Bedeutung von Gleichung (9):
Der resultierende thermische Wirkungsgrad eines "de-idealisierten" Stirlingprozesses - das ist ein isothermer Stirlingprozess mit einem verlustbehafteten Regenerator- ist als Funktion zu sehen von:
- k = 1.6 für ein-atomige Gase wie Helium, Argon,
- k = 1.4 für zwei-atomige Gase wie Wasserstoff, Luft, Stickstoff
- k = 1.3 für drei-atomige Gase wie Kohlendioxyd CO 2
Diese Abhängigkeiten des thermischen Wirkungsgrades zeigt
Abb.1.
Abszisse
ist der Carnot- Wirkungsgrad h c
= (TE - TC) / TE im Bereich von
5 <= h c
<= 80%.
Die Ordinate ist der mit Gleichung (9) berechnete thermische
Wirkungsgrad.
Abb.1 wurde berechnet
Das in Abb.1 eingezeichnete Beispiel besagt:
Wenn die Temperaturen eines "de-idealisierten" Stirlingprozesses "TE" und "TC" bekannt sind, sodass sich mit TE und TC ein Carnot Wirkungsgrad von hC = 28 % ergibt, und man die Maschine für ein Volumenverhältnisse Vmax / Vmin = 1.6 ausgelegt hat und sie mit einem Regenerator versieht, dessen Wirkungsgrad hreg = 50 % ist -also mit einem Regeneratorverlust von RV = 50 %- dann wird der thermische Wirkungsgrad dieses Prozesses htherm = 16 % sein.
Ein 2. Ergebnis dieser Beispiel Rechnung ist:
Man wird den gleichen thermischen Wirkungsgrad htherm = 16 % bekommen, wenn man das Volumenverhältnis auf Vmax / Vmin = 2.5 erhöhen kann; dann kann auf den Regenerator verzichtet werden, bzw er braucht nur ein Verbindungsrohr zu sein. Die Kurve in Abb.1 für Vmax / Vmin = 1.6 und hreg = 50 % deckt sich ziemlich gut mit der Kurve für Vmax / Vmin = 2.5 und hreg = 0 %.
Mit Abb.2 wird der Einfluss von k des Arbeitsgases demonstriert. Das Diagramm ist berechnet für die gleichen 5 Volumenverhältnisse Vmax / Vmin = 1.2, 1.6, 2.5, 5.0, und 10.0 wie das Diagramm in Abb.1. Desweiteren wurde dieses Diagramm für das Edelgas Argon mit k = 1.6, und für Luft mit k= 1.4 berechnet. Bei Argon soll der Regeneratorwirkungsgrad hreg = 20 % sein und für Luft soll die Maschine mit einem Regenerator ausgestattet sein, dessen Wirkungsgrad sei h reg = 45 %. Diese beiden Regeneratorwirkungsgrade sind speziell gewählt worden um zu demonstrieren, dass man bei gleichem Volumenverhältnis 2'er zu vergleichender Maschinen mit einem schlechter wirkenden Regenerator - wenn man Argon als Arbeitsgas wählt- den gleichen thermischen Wirkungsgrad in der Maschine bekommt, wie wenn man das 2-atomige Gas Luft als Arbeitsfluid und einen besser wirkenden Regenerator wählt. Der zusätzliche Gewinn trotz eines schlechter wirkenden Regenerators besteht darin, dass in ihm weniger Druckverlust entsteht, als in einem Regenerator, der wegen seiner dichten Packung einen besseren Wirkungsgrad aber auch einen höheren Druckverlust hat.
Die Aussage von Gleichung (9) ist jedoch mit Vorsicht zu interpretieren; denn Gl. (9) kann nicht die Wärmeleitfähigkeit des Arbeitsfluids berücksichtigen, die ja auch sehr wesentlich den thermischen Wirkungsgrad mitbestimmt. Dennoch wird diese Aussage Bestand haben für eine langsam laufende Maschine, wie sie in |1| beschrieben ist, die einen optimalen Wärmeübergang auf das Arbeitsfluid innerhalb der Arbeitszylinder ermöglicht. Hier dürfte Argon, trotz seiner etwas schlechteren Wärmeleitfähigkeit als Luft gemäss Gl. (9) das bessere Arbeitsfluid darstellen. Natürlich wird das teurere Edelgas Helium neben der Aussage von Gl. (9) auch wegen seiner ca. 4 mal besseren Wärmeleitfähigkeit als Luft zu einem noch besseren thermischen Wirkungsgrad führen.
Für die in |1| beschriebene Maschine ist ein in FORTRAN 77 geschriebenes Computerprogramm STMOT2 entwickelt worden. Dieses Programm ermöglicht die Berechnung, graphische Ausgabe und Druckausgabe von mehr als 230 verschiedenen Grössen, die für eine Stirlingmaschine von Interesse sind |6|. Mit diesem Programm sind die beiden T-S Diagramme Abb.3 und Abb.4 errechnet worden. In Abb.3 ist mit Luft k =1.4 und in Abb.4 ist mit Argon k =1.6gerechnet worden. Die "Rahmen" in beiden T-S Diagrammen repräsentieren den idealen isothermen Stirling Prozess, der Kurvenzug innerhalb eines Rahmens stellt den realen Prozess dar, wie er sich für die a - Maschine mit Kurbeltrieb und 90 Grad Winkelversatz zwischen Expansions- und Kompressionsbewegung ergibt. In beiden Fällen repräsentieren jeweils die Kurvenzüge und jeweils die "Rahmen" die gleiche Nutzarbeit pro Umdrehung. Die Wirkung der unterschiedlichen Adiabatenexponenten k der beiden Arbeitsgase ist in der Steigung der Isochoren -Linienzüge 2-3 und 4-1 zu sehen. Für diese Steigung d T/d S ergibt sich:
(10) 
Die Steigung der Isochoren d T / d S ist also auch eine Funktion von k der Art des Arbeitsgases. Für den idealen Prozess in Abb.4 ist der isochore Energieaustausch des Regenerators durch die Fläche unter der Linie 1-4 mit der Abszisse dargestellt. Man erkennt den deutlich höheren isochoren Energiebetrag mit Luft als Arbeitsgas unter der Linie 1-4 in Abb.3. In dem Kurvenzug für den realen Prozess ist der isochore Energieaustausch des Regenerators nicht so deutlich zu erkennen. Hier ergibt jedoch die Berechnung entsprechend unterschiedliche Werte. So erhöht sich der thermische Wirkungsdgrad htherm des berechneten realen Prozesses von htherm = 20.6 % mit Luft als Arbeitsgas (Abb.3) aufhtherm = 23.7 %, wenn Argon als Arbeitsgas (Abb.4) gewählt wird.
Berechnet man den thermischen Wirkungsgrad nach Gl (9) für den "de-idealisierten" isothermen Stirlingprozess (das sind die "Rahmen" in Abb.3 und 4), dann ergibt sich eine Verbesserung von htherm = 25.6% (Arbeitsgas Luft Abb.3) auf htherm = 29.1 % mit Argon als Arbeitsgas (Abb.4).
Diese Rechnungen wurden durchgeführt mit:
Weitere 8 Rechnungen sind mit dem Computerprogramm STMOT2 gemacht worden, um den Einfluss des Ruhedruckes P0 (das ist der Gasdruck in der stillstehenden kalten Maschine), des Volumenverhältnisses Vmax/Vmin, des Adiabatenexponenten k sowie des Regeneratorwirkungsgrades hreg auf die Nutzleistung und den Nutzwirkungsgrad h_n der Maschine zu zeigen. Die Ergebnisse sind tabellarisch zusammen gefasst. (Nähere Einzelheiten zur Ausgabe von STMOT2 siehe in |6|. Die Eingabedaten zu dieser Berechnung sind in den "Fallstudien" beschrieben; der interessierte Leser kann sich hier die Eingabedatensätze kopieren und die Berechnungen nachvollziehen.)
In der Tabelle sind die hier interessierenden Grössen für das Arbeitsfluid Helium rot und für Luft blau hervorgehoben. Folgende Erläuterungen zu dieser Tabelle sind noch zu machen:
In Spalte 1 der Tabelle weist
RUN NO. auf den jeweiligen Rechenlauf hin.
In Spalte 7 ist ETA_R
der Regenerator Wirkungsgrad hreg
In Spalte 9 ist P0
der Ruhedruck in der stillstehenden kalten Maschine, P1MEAN
ist der mittlere Arbeitsdruck
In Spalte 10 ist Vmax/Vmin das Volumenverhätnis,
In Spalte 13 ist ETA_N der Nutzwirkungsgrad,
der in der Beschriftung der Abb.(1)(2) und Abb.(5)(6) mit
h_n bezeichnet ist.
In Spalte 15 ist POWER USABLE die Nutzleistung.
In Spalte 16 wird mit
DQZU1 MAX die maximale Heizleistung wärend
der gerechneten Umdrehung angegeben.
Weitere Erläuterungen zu der Tabelle sind dem Kapitel I.6.2 der Programmbeschreibung von
STMOT2 zu entnehmen.
Die ersten 4 Rechenläufe betreffen die Steigerung der Nutzleistung POWER USABLE als Folge eines höheren Volumenverhältnisses. Rechenläufe (1) und (2) sind für Luft mit k = 1.4 und Rechenläufe (3) und (4) sind für Helium mit k = 1.6 durchgeführt worden. Zur Verdeutlichung, hier ein Auszug aus der Tabelle.
Die beträchtliche Leistungssteigerung von POWER = 343 Watt in den Rechenläufen
(2) und (4) auf POWER = 1637 Watt
in den Rechenläufen (1) und (3)
ist natürlich nur zu realisieren, wenn "Erhitzer" und
"Kühler" die erhöhten Energietransporte auch aufbringen
können !!
Die Maximalwerte für die Heizleistung "DQZU1 MAX" sind jeweils der
Spalte 16: in untenstehender
Tabelle zu entnehmen.
Mit Helium als Arbeitsfluid ist, hier wie nach Gleichung (9)
zu erwarten, ein kleinerer Maximalwert "DQZU1 MAX" errechnet worden.
Den Verlauf der Heizleistung "DQZU1" und der Kühlleistung "DQAB1", der mittleren Nutzleistung der Maschine "POWERN" für die betrachtete Umdrehung und den Verlauf des Gasdruckes "P1" als Funktion des Kurbelwinkels zeigt die Abb.(1)(2). Hier sind die Rechenläufe (1) und (2) für Luft als Arbeitsfluid zusammen in 1 Diagramm wiedergegeben. Die Markierungen (1) und (2) in Abb.(1)(2) entsprechen diesen Rechenläufen. Sie entsprechen auch den RUN NO. Einträgen 1 und 2 in untenstehender Tabelle. Die Werte für Helium können der Tabelle bei RUN NO. 3 und 4 entnommen werden.
In den nächsten 4 Rechenläufen (5) und (6) für Luft und (7) und (8) für Helium soll die Nutzleistung der Maschine bei ca. 316 bis 319 Watt konstant bleiben. Es soll hier gezeigt werden, dass bei einem hohen Volumenverhältnis Vmax / Vmin =2.71 diese nahezu gleiche Leistung erreicht werden kann mit einem deutlich geringerem Ruhedruck "P0"=3.3 bar -bzw. mittlerem Arbeitsdruck "P1MEAN"- und einem niedrigerem Regeneratorwirkungsgrad hreg=40 % als sie bei einem kleinerem Volumenverhältnis Vmax / Vmin =1.29 erreicht wird mit P0=15 bar und hreg = 80%. Daneben ergibt die Rechnung, dass die maximal zuzuführende Heizleistung erheblich geringer wird, wenn die Maschine bei dieser Nutzleistung von 316 - 319 Watt mit einem hohen Volumenverhältnis arbeitet. Hier wieder zur Verdeutlichung ein Auszug aus der Tabelle.
Diese Ergebnisse scheinen auf den ersten Blick unwahrscheinlich zu sein.
Eine wichtige Darstellung zur Erläuterung des Phänomens der Ergebnisse dieser Rechenläufe (5) und (6) für Luft als Arbeitsfluid bieten die T-S Diagramme in
Abb.(5)(6)TS, und für die
Rechenläufe (7) und (8) für Helium
bieten die T-S Diagramme in Abb.(7)(8)TS hier eine Erklärung:
Die Arbeit, die pro Umdrehung in der Maschine verrichtet wird, wird durch die Fläche repräsentiert, die durch die jeweiligen Kurven eingeschlossen werden. Diese Arbeit -abzüglich der Reibungsverluste resultiert in Nutzleistung: 316 bzw. 319 Watt.
Die Flächen, die durch die "Rahmen" um die Kurven gebildet werden, entsprechen der Arbeit des idealen Stirlingprozesses. Betrachten wir nur die idealen Stirlingprozesse für die
Rechenläufe (5) und (6) (oder für die Rechenläufe
(7) und (8)), dann ergibt sich in der Tat ein ganz anderes Ergebnis. Die Arbeit "Wi" des idealen Stirlingprozesses entspricht dem Zähler in Gl. (8) -siehe oben:
Wi = M Gas * R * (TE - TC) * ln ( V max / V min )
wobei die Gasmasse "M Gas" proportional dem Ruhedruck P0 ist. So ist auch die Arbeit des idealen Stirlingprozesses aus Rechenlauf (6) mit dem hohen Ruhedruck P0 = 15 bar deutlich höher als bei Rechenlauf (5) mit P0 = 3.3 bar, wie sich unschwer aus dem Vergleich beider "Rahmen" in den beiden Diagrammen der Abb.(5)(6)TS (als auch in beiden Diagrammen der Abb.(7)(8)TS) erkennen lässt. Der idealen Stirlingprozesses kennt keine Toträume, die im realen Stirlingprozesses, in dem auch noch ein kontinuierlich arbeitender Kurbeltrieb wirkt, sehr wohl berücksichtigt werden müssen. Im realen Stirlingprozess wirkt sich nun ein hohes Volumenverhältnis -d.h. wenig Totraum- dahingehend aus, dass auch ein hoher "Ausnutzungsgrad" -hier 37.11%- zum idealen Stirlingprozess erreicht wird. (Zum "Ausnutzungsgrad" siehe auch meinen ungekürzten Bericht zur 6. ISEC in Eindhoven |1|.) Der erhebliche Totraum, der in den Rechenläufen (6) und (8) eingegeben wurde, führt nun hier zu einem geringen Ausnutzungsgrad -hier 8.73%- des maximal möglichen -idealen- Prozesses, sodass sich hier trotz höherem Arbeitsdruck bzw. Ruhedruck P0 fast nur die gleiche Arbeit ergibt wie in den Rechenläufen (5) und (7). In Spalte 13 der Tabelle ist mit AUSN_I dieser Ausnutzungsgrad angegeben.
Da im Rechenlauf (5) mit GM01= 1.394851 gr Luft erheblich weniger Gasmasse in der Maschine ist als in Rechenlauf (6) mit GM01= 23.520571 gr Luft (siehe unter den Spalten 17 - 19 in der Tabelle) wird auch die Heizleistung für diese Gasmasse geringer sein. Die maximale Heizleistung wird in Spalte 16 der Tabelle mit "DQZU1_MAX" = 2496 Watt errechnet, während für Lauf (6) die maximale Heizleistung mit "DQZU1_MAX" = 5266 Watt errechnet wird.
Abb.(5)(6) zeigt den Verlauf der Heizleistung "DQZU1" und der Kühlleistung "DQAB1", die mittlere Nutzleistung der Maschine "POWERN" für die betrachtete Umdrehung und den Verlauf des Gasdruckes "P1" als Funktion des Kurbelwinkels. Hier sind die Rechenläufe (5) und (6) wiederum für Luft als Arbeitsfluid zusammen in 1 Diagramm wiedergegeben. Die Markierungen (5) und (6) in Abb.(5)(6) entsprechen diesen Rechenläufen. Sie entsprechen auch den RUN NO. Einträgen 5 und 6 in untenstehender Tabelle. Die Werte für Helium können der Tabelle bei RUN NO. 7 und 8 entnommen werden.
Der Nutzwirkungsgrad ETA_N in Spalte 13 der Tabelle wird in der Beschriftung zu Abb.(1)(2) und Abb.(5)(6) mit "h_n" bezeichnet. In der Beschriftung von Abb.(5)(6) sind die Werte für h_n eingesetzt, diese können auch in der Tabelle unter RUN NO. (5) und (6) abgelesen werden. Beachtenswert ist, dass der Nutzwirkungsgrad h_n mit 19.59 % in RUN NO. 5 sogar grösser ist als in RUN NO. 6 mit 17.89 % obglgleich der Regeneratorwirkungsgrad in RUN NO. 5 mit hreg= 40 % nur halb so gross ist wie hreg= 80 % in RUN NO. 6. (Diese Nutzwirkungsgrade "h_n" sowie die Nutzleistung POWERN berücksichtigen auch die mechanischen Reibungsverluste der Maschine. "h_n" ist darum kleiner als htherm.)
Zusammenfassung:
Um in a- Typ Stirlingmaschinen, die mit niedrigen bis mittleren Temperaturdifferenzen arbeiten, eine möglichst hohe Nutzarbeit pro Umdrehung zu erzielen, ist ein hohes Volumenverhältnis Vmax/Vmin nötig. Dies gilt insbesondere für solche Maschinen, die mit niederen bis mittleren Temperaturdifferenzen arbeiten, wie die in |1| beschriebene Maschine. Eine Erhöhung des Volumenverhältnisses bringt trotz eines verlustbehafteten Regenerator auch eine Verbesserung des thermischen Wirkungsgrades. Grundsätzlich wird der Regenerator besonders verlustbehaftet sein bei Maschinen, die mit "compound Fluids" arbeiten, deren eine Komponente kondensierender Dampf ist. Eine Möglichkeit, den Regeneratorverlust auszugleichen und somit den thermischen Wirkungsgrad anzuheben, ist bei doppelt wirkenden Maschinen gegeben durch Kombination 2'er Regeneratoren zu einem Gegenstrom Wärmetauscher, wie es bei der Maschine in |1| ausgeführt wird. Eine weitere Möglichkeit, wie hier gezeigt, besteht darin, ein 1-atomiges Edelgas anstelle eines mehr atomigen Gases als Arbeitsfluid zu wählen. (Ob in diesem Sinn Helium besser als Wasserstoff mit seiner doppelt so guten Wärmeleitfähigkeit ist, müssten entsprechende Versuche ergeben) . Des weiteren kann die Nutzarbeit pro Umdrehung erhöht werden, wenn man nach den in |2| aufgestellten Regeln das Verhältnis der Hubvolumina von Expansions- und Kompressionszylinder den Temperaturverhältnissen angleicht: Ve / Vc = TE / TC, siehe hierzu auch die Beispielrechnung in den Fallstudien .
Obige Gleichung (9) ist für einen "de-idealisierten" isothermen Stirling Prozess abgeleitet worden, dessen isochore Wärmeübertragung jeweils bei konstantem Volumen erfolgt. Bezüglich des thermischen Wirkungsgrades htherm , des Volumenverhältnisses Vmax / Vmin und k , sind die Berechnungen für die Maschine nach |1| mit Kurbeltrieb -also mit einer kontinuierlichen Volumenänderung- durchaus zu vergleichen mit den Rechenergebnissen nach Gleichung (9); denn die Voraussetzungen des Prozesses in dieser Maschine sind denen des "de-idealisierten" isothermen Stirling Prozesses ähnlich:
Anders sind allerdings die Verhältnisse bei dem mehr polytrop ablaufenden Prozess in den herkömmlichen Stirling Maschinen vom b oder g Typ. Auf die Arbeitsräume dieser Maschinen können die Gleichungen (5) bis (9) nicht angewendet werden.
Für die Berechnung des Prozesses der a - Maschine nach |1| seien folgende Überlegungen zur Diskussion gestellt:
Die isotherme Zustandsänderung ist definiert durch:
![]()
Die adiabate Zustandsänderung ist definiert durch:
![]()
Die polytrope Zustandsänderung ist definiert durch:
![]() mit dem Exponenten n < k
mit dem Exponenten n < k

Der Exponent e ist kleiner als
k für die adiabate bzw.
auch kleiner als n für die polytrope
Zustandsänderung. Weil in diesem Prozess Wärmezufuhr
und Kühlung extrem gut innerhalb der Arbeitszylinder erfolgen,
liegt der Exponent e im Bereich 1 <
e << n.
Es kann e nahe= 1 gesetzt werden.
Um die Richtigkeit dieses Ansatzes zu prüfen, sollten
entsprechende Messungen an der Maschine gemacht werden.
Als eine Ableitung aus obigen Formeln ergibt sich zur Temperaturberechnung die Beziehung:
(11)

Eine weitere Annahme, die bei der Berechnung des Prozesses gemacht wurde, darf nicht verschwiegen werden: Der Druckverlust im Regenerator wurde vernachlässigt, sodass mit dem gleichen momentanen Druck des Arbeitsgases in allen Volumina gerechnet wurde. Für diese Annahme gibt es aber auch Gründe:
Literatur:
|1| P.Fette: A Stirling Engine Able to Work with Compound Fluids Using Heat Energy of Low to Medium Temperatures. Presented at the 6'thISEC in Eindhoven 1993; ISEC-93-003
|2| T. Finkelstein: Theoretical Considerations: The Concept of the "Cumulative Mass" and "Thermodynamic Mid-Plane" and the Resulting Volume Ratios, Europeen Stirling Forum Osnabrück 1994
|3| G. Walker: Stirling Engines, Clarendon Press Oxford 1980
|4| R.J.Meijers: Der Philips Stirlingmotor, Motoren Technische Zeitschrift MTZ 29(1968)/7, DK 621.41/43 (492) Philips
|5| P.Fette: Neuer Wärmekraftprozess für die Nutzung von Niedertemperatur Wärme, Brennstoff Wärme Kraft Bd.39 1987 Nr.11, VDI Verlag Düsseldorf
|6| P.Fette: STMOT2 Ein Computerprogram zur Berechnung des Waermekraftprozesses und der Dynamik von Alpha-Typ Stirlingmotoren
|7| P. Fette Grundlagen für die Berechnung des Wärmekraftprozesses und der Dynamik von a -Typ Stirlingmotoren mit dem Programm STMOT2
Fragen ?
Abb.1 Der Effekt von V max / V min und des Regenerator Wirkungsgrades hreg auf den Thermischen Wirkungsgrad htherm
Die obere schwarze Gerade mit den 3 blauen Rechtecken gilt für h reg = 100 % und für alle Vmax / Vmin und für alle k's
Benutzen Sie den Zurück Schaltknopf Ihres Browsers, um an die vorige Textstelle zurückzu kommen
Abb.2 Der Effekt von V max / V min und des Adiabaten Exponents k = C p / C v auf den Thermischen Wirkungsgrad htherm
Benutzen Sie den Zurück Schaltknopf Ihres Browsers, um an die vorige Textstelle zurückzu kommen
Benutzen Sie den Zurück Schaltknopf Ihres Browsers, um an die vorige Textstelle zurückzu kommen
-
Vielleicht deutlicher als die Abb.(1)(2) und Abb.(5)(6) zeigt die folgende Tabelle die Ergebnisse der Berechnungen. Diese Tabelle ist mit dem Programm STMOT2 erstellt worden.
____________________________________________________________________________________________________________________________________
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20
___|_____|____|______|______|______|______|______|______|_____|_____|_______|_______|______|_____|_____|______|______|______|______
RUN| DKST|KAPA| TEMP.|STROKE| DEAD |REGEN.| DEAD | P0 |VMAX |PMAX | WORK | WORK |- WORK|POWER|DQZU1|DIFFERENCE IN GASMAS|TIME .
No.| DH |EXP | TH | VOL. | VOL. | VOL. | VOL. | | / | / | A1 | A2 |LOST |USABL| MAX | EXP. | COMP.| REG. | sec
| DK |COMP| TK | EXP. | EXP. | | COMP.| |VMIN |PMIN | |Watt*s | | | | | | |
STROKE| |TE_MAX| COMP.| |cm**3 | |P1MEAN| | | | | | | | | | |REVOL.
RE-| | |TC_MIN| | | | | | | | | ETA_N | | | | | | |TIME
VOL| | | | | | ETA_R| | | | | | AUSN_I| | | | | | | msec
| | | | | | | | | | | | AREF_I| | | | | | |
|cm | - |Kelvin|cm**3 |cm**3 | % |cm**3 | Bar | - | - |Watt*s | % |Watt*s| Watt| Watt|Gramm |Gramm |Gramm |RPM
---|-----|----|------|------|------|------|------|------|-----|-----|-------|-------|------|-----|-----|------|------|------|------
1| 2.00|1.00| 500.0| 251.3| 10.1| 100.0| 10.1|16.000|2.710|2.832| 156.8| 154.81|11.146| 1637| 9124| 3.504| 4.173| 2.177| 0.375
| 8.00|1.00| 300.0| 235.6| | | | | | | | | | | | | | |
| 8.00| | | | | | | | | | |30.46 %| | | | | | | 374.7
| 5.00| | 500.0| | | 80.0| | 22.58| | | |39.62 %| | | |GM01= 6.762916 Gr |
1| | | 300.0| | | | | | | | |22.40 %| | | |TOTAL GASMASS | 160.2
| | | | | | | | | | | | | | | | | | |
___|_____|____|______|______|______|______|______|______|_____|_____|_______|_______|______|_____|_____|______|______|______|______
2| 2.00|1.00| 500.0| 251.3| 502.7| 100.0| 502.7|16.000|1.290|1.297| 35.0| 34.84|11.144| 343| 5618| 3.061| 3.161| 0.465| 0.375
| 8.00|1.00| 300.0| 235.6| | | | | | | | | | | | | | |
| 8.00| | | | | | | | | | |17.99 %| | | | | | | 374.9
| 5.00| | 500.0| | | 80.0| | 20.13| | | | 8.78 %| | | |GM01= 25.088609 Gr |
1| | | 300.0| | | | | | | | | 1.27 %| | | |TOTAL GASMASS | 160.0
| | | | | | | | | | | | | | | | | | |
___|_____|____|______|______|______|______|______|______|_____|_____|_______|_______|______|_____|_____|______|______|______|______
3| 2.00|1.00| 500.0| 251.3| 10.1| 100.0| 10.1|16.000|2.710|2.832| 156.8| 154.81|11.146| 1637| 8598| 0.484| 0.576| 0.301| 0.375
| 8.00|1.00| 300.0| 235.6| | | | | | | | | | | | | | |
| 8.00| | | | | | | | | | |33.39 %| | | | | | | 374.7
| 5.00| | 500.0| | | 80.0| | 22.58| | | |39.62 %| | | |GM01= 0.933516 Gr |
1| | | 300.0| | | | | | | | |22.40 %| | | |TOTAL GASMASS | 160.2
| | | | | | | | | | | | | | | | | | |
___|_____|____|______|______|______|______|______|______|_____|_____|_______|_______|______|_____|_____|______|______|______|______
4| 2.00|1.00| 500.0| 251.3| 502.7| 100.0| 502.7|16.000|1.290|1.297| 35.0| 34.84|11.144| 343| 5308| 0.422| 0.436| 0.064| 0.375
| 8.00|1.00| 300.0| 235.6| | | | | | | | | | | | | | |
| 8.00| | | | | | | | | | |22.47 %| | | | | | | 374.9
| 5.00| | 500.0| | | 80.0| | 20.13| | | | 8.78 %| | | |GM01= 3.463093 Gr |
1| | | 300.0| | | | | | | | | 1.27 %| | | |TOTAL GASMASS | 160.0
| | | | | | | | | | | | | | | | | |
___|_____|____|______|______|______|______|______|______|_____|_____|_______|_______|______|_____|_____|______|______|______|______
5| 2.00|1.00| 500.0| 251.3| 10.1| 100.0| 10.1| 3.300|2.710|2.841| 32.6| 32.14|11.144| 316| 2496| 0.725| 0.863| 0.448| 0.375
| 8.00|1.00| 300.0| 235.6| | | | | | | | | | | | | | |
| 8.00| | | | | | | | | | |19.59 %| | | | | | | 374.9
| 5.00| | 500.0| | | 40.0| | 4.67| | | |37.11 %| | | |GM01= 1.394851 Gr |
1| | | 300.0| | | | | | | | |20.98 %| | | |TOTAL GASMASS | 160.0
| | | | | | | | | | | | | | | | | | |
___|_____|____|______|______|______|______|______|______|_____|_____|_______|_______|______|_____|_____|______|______|______|______
6| 2.00|1.00| 500.0| 251.3| 502.7| 100.0| 502.7|15.000|1.290|1.297| 32.8| 32.66|11.144| 319| 5266| 2.869| 2.963| 0.436| 0.375
| 8.00|1.00| 300.0| 235.6| | | | | | | | | | | | | | |
| 8.00| | | | | | | | | | |17.89 %| | | | | | | 374.9
| 5.00| | 500.0| | | 80.0| | 18.87| | | | 8.73 %| | | |GM01= 23.520571 Gr |
1| | | 300.0| | | | | | | | | 1.26 %| | | |TOTAL GASMASS | 160.0
| | | | | | | | | | | | | | | | | | |
___|_____|____|______|______|______|______|______|______|_____|_____|_______|_______|______|_____|_____|______|______|______|______
7| 2.00|1.00| 500.0| 251.3| 10.1| 100.0| 10.1| 3.300|2.710|2.841| 32.6| 32.14|11.144| 316| 2135| 0.100| 0.119| 0.062| 0.375
| 8.00|1.00| 300.0| 235.6| | | | | | | | | | | | | | |
| 8.00| | | | | | | | | | |23.92 %| | | | | | | 374.9
| 5.00| | 500.0| | | 40.0| | 4.67| | | |37.11 %| | | |GM01= 0.192538 Gr |
1| | | 300.0| | | | | | | | |20.98 %| | | |TOTAL GASMASS | 160.0
| | | | | | | | | | | | | | | | | | |
___|_____|____|______|______|______|______|______|______|_____|_____|_______|_______|______|_____|_____|______|______|______|______
8| 2.00|1.00| 500.0| 251.3| 502.7| 100.0| 502.7|15.000|1.290|1.297| 32.8| 32.66|11.144| 319| 4977| 0.396| 0.409| 0.060| 0.375
| 8.00|1.00| 300.0| 235.6| | | | | | | | | | | | | | |
| 8.00| | | | | | | | | | |22.34 %| | | | | | | 374.9
| 5.00| | 500.0| | | 80.0| | 18.87| | | | 8.73 %| | | |GM01= 3.246650 Gr |
1| | | 300.0| | | | | | | | | 1.26 %| | | |TOTAL GASMASS | 160.0
| | | | | | | | | | | | | | | | | | |
___|_____|____|______|______|______|______|______|______|_____|_____|_______|_______|______|_____|_____|______|______|______|______
Benutzen Sie den Zurück Schaltknopf Ihres Browsers, um an die vorige Textstelle zurückzu kommen
Abb.(1)(2) Der Einfluss des Volumenverhältnisses auf die zuzuführende Leistung "DQZU1" und auf die Nutzleistung "POWERN" der Maschine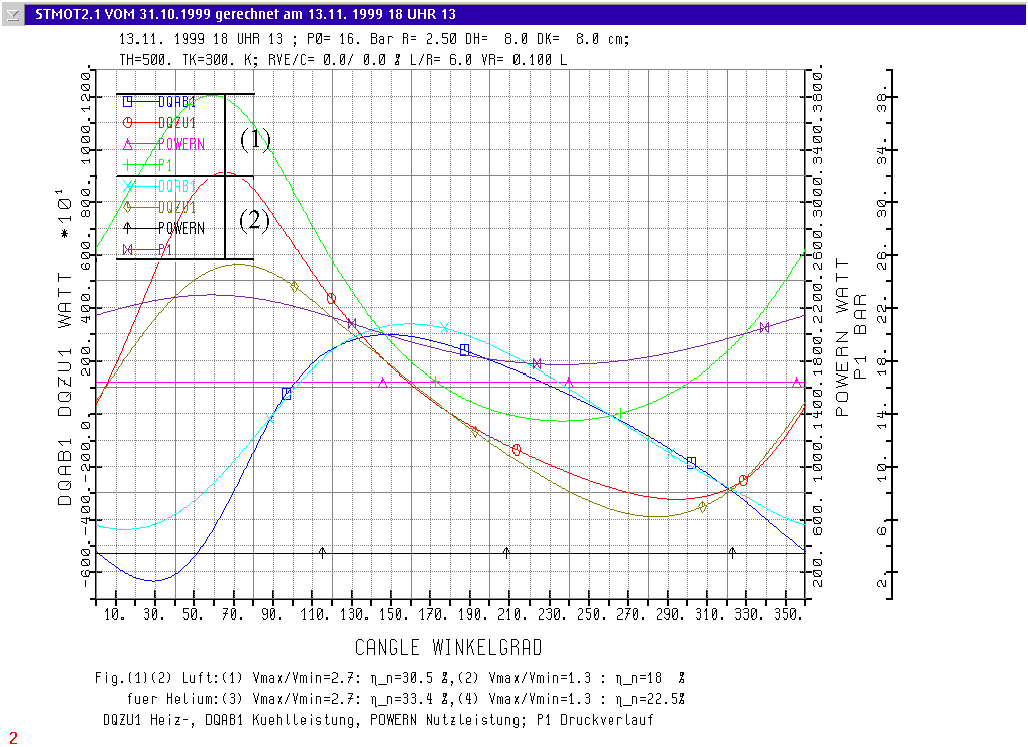
Benutzen Sie den Zurück Schaltknopf Ihres Browsers, um an die vorige Textstelle zurückzu kommen
-
Abb.(5)(6) Der Einfluss des Volumenverhältnisses, des Regenerator - Wirkungsgrades und des Ruhedrucks P0 auf die Nutzleistung "POWERN" der Maschine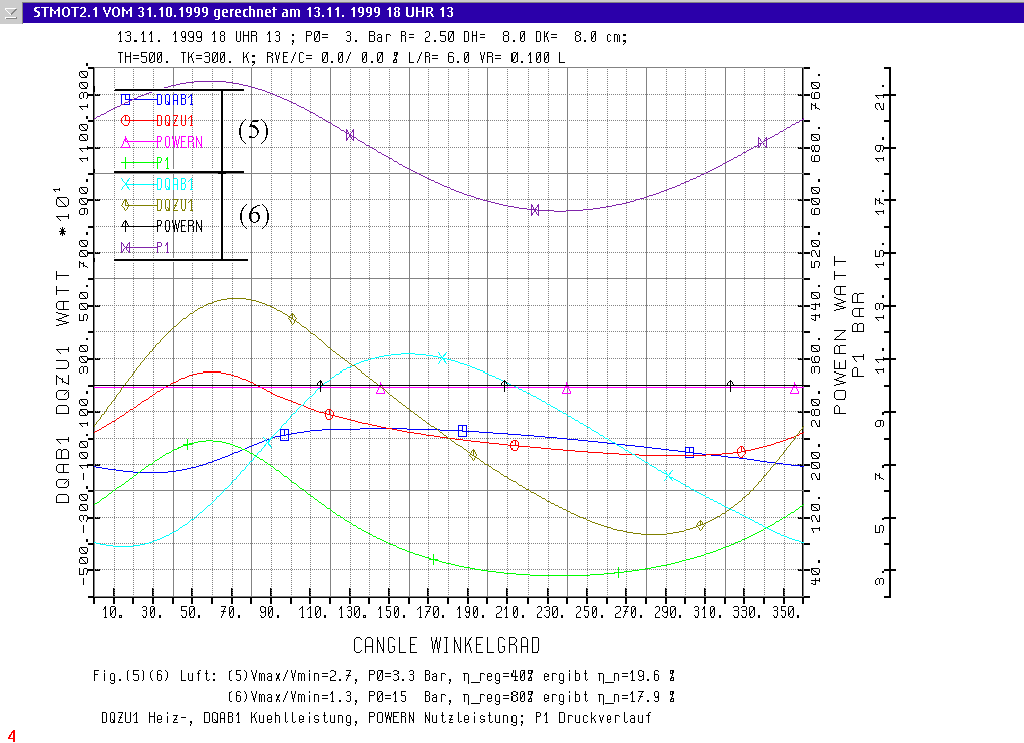
Benutzen Sie den Zurück Schaltknopf Ihres Browsers, um an die vorige Textstelle zurückzu kommen
-
Abb.(5)(6)TS T-S Diagramme für Luft: Rechenlauf (5) mit hohemVolumeverhältnis Vmax/Vmin =2.71 und Lauf (6) mit niedrigem Volumeverhältnis Vmax/Vmin =1.29; die "Rahmen" entsprechen dem idealen Stirlingprozess. Ergebnisse der Berechnung siehe in der Tabelle unter RUN NO. 5 und 6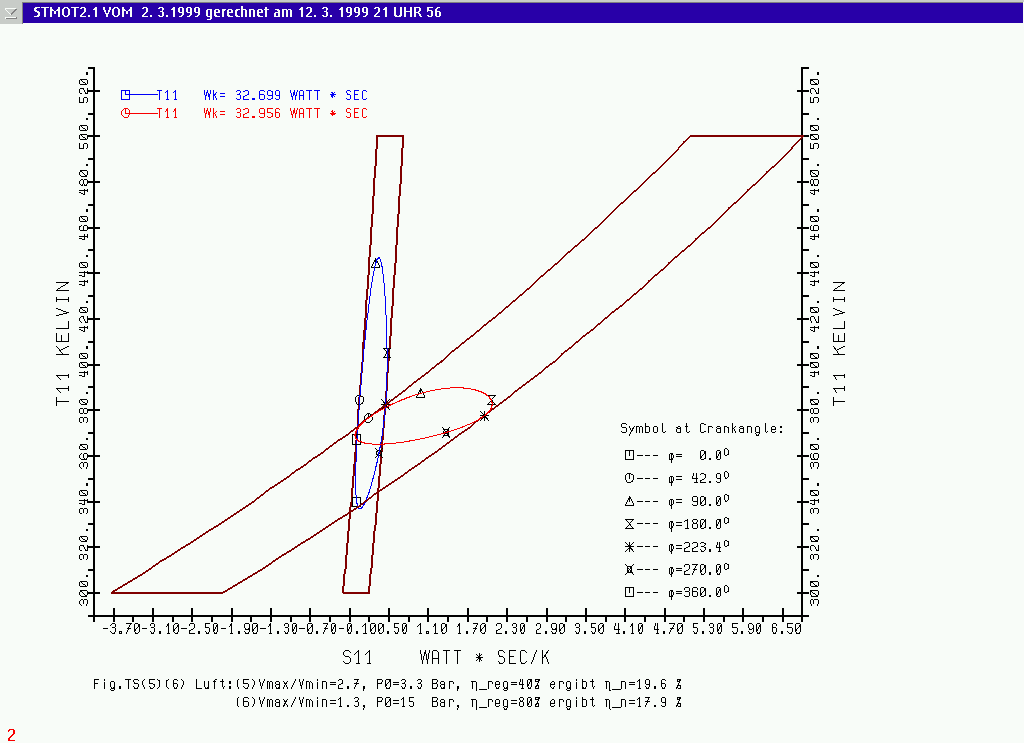
Benutzen Sie den Zurück Schaltknopf Ihres Browsers, um an die vorige Textstelle zurückzu kommen
-
Abb.(7)(8)TS T-S Diagramme für Helium Rechenlauf (7) mit hohemVolumeverhältnis Vmax/Vmin =2.71 und Lauf (8) mit niedrigem Volumeverhältnis Vmax/Vmin =1.29; die "Rahmen" entsprechen dem idealen Stirlingprozess. Ergebnisse der Berechnung siehe in der Tabelle unter RUN NO. 7 und 8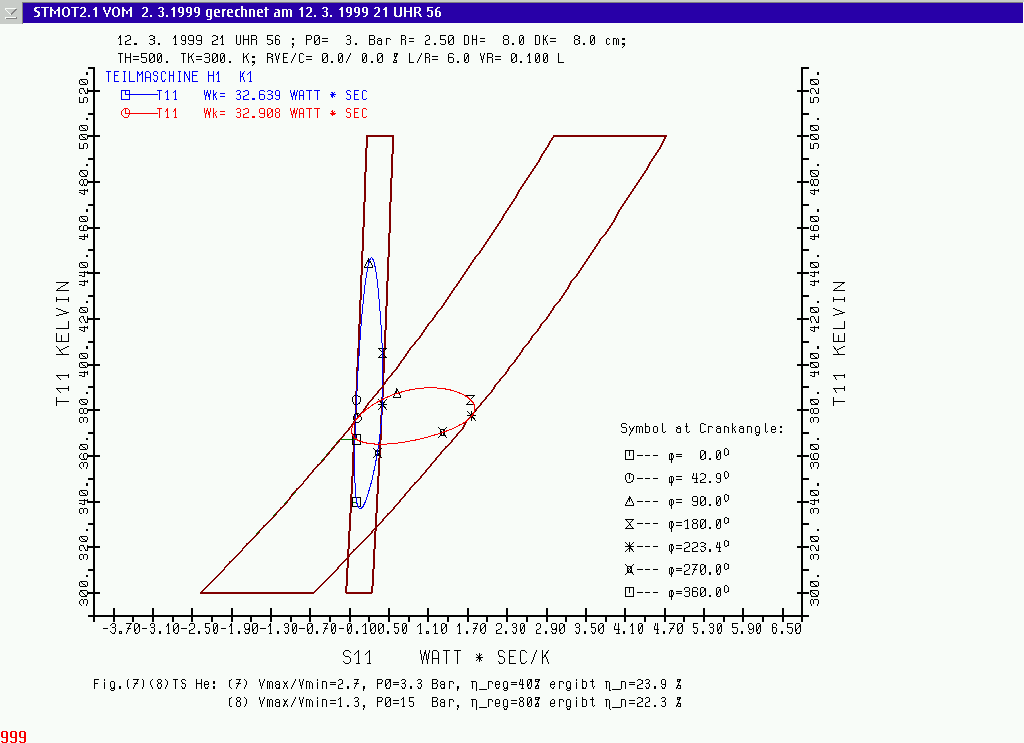
Benutzen Sie den Zurück Schaltknopf Ihres Browsers, um an die vorige Textstelle zurückzu kommen
Fragen ?