Berechnung des Solarstrom Deckungsgrades einer PV-Anlage mit Stromspeicher
Achtung: Diese Seite befindet sich noch im Aufbau
Inhaltsverzeichnis
Heute kann kein Windpark und kein grosser PV-Solarpark rund um die Uhr Strom liefern. Konventionelle Kraftwerke sind immer noch nötig, um Lücken in der Stromversorgung auszugleichen, die infolge von Flaute bei den Windparks bzw. noch dramatischer bei den Solarparks während der Nacht und bei bewölktem Himmel entstehen. Wenn die Energiewende erfolgreich sein soll, müssen grosse und preiswerte Stromspeicher entwickelt werden.
Dieser Bericht zeigt die Abhängigkeit von Solarspeicher Kapazität, PV-Modulfläche, einem Datensatz der täglichen PV-Einstrahlung auf die Modulfläche und den täglichen Stromverbrauch auf den Deckungsgrad der Eigenstromnutzung eines Haushalts. Das Rechenprogramm, was diese Abhängigkeit sichtbar macht, kann ebensogut mit einem Datensatz des täglichen Windstrom Gewinns arbeiten.
Man kann mit diesem Computer-Programm iterativ einen gewünschten Deckungsgrad der
Eigenstromversorgung einer bestehenden (oder auszulegenden) PV-Anlage berechnen.
Voraussetzung für die Berechnung ist ein Datensatz der täglichen PV-Einstrahlung und des täglichen
Stromverbrauchs über eine Abrechnungsperiode.
Standort der PV-Anlage, von der Datensätze existieren, ist Walzbachtal in der Nähe von Karlsruhe.
Zweckmässigerweise beginnt ein Datensatz mit dem 1. Juni und endet am 31. Mai des Folgejahres.
Es gibt also 365 Zeilen in jedem Datensatz für 365 Tage. Der Beginn am 1. Juni ist nicht ohne Grund
festgelegt; zu diesem Zeitpunkt herrscht meistens beständiger Sonnenschein und der Solarspeicher kann von seinem Anfangswert
an aufgeladen werden. Würde man den Datensatz am 1. Januar beginnen, dann hätte man keinen
kontinuierlichen Übergang von einer zur nächsten 365 Tage währenden Berechnungsperiode. Man könnte
keinen Speicher für einen 100% Deckungsgrad definieren.
Die Datensätze mit den täglichen Einträgen der Zählerstände von PV-Strom am Wechselrichter und vom
Stromzähler bestehen seit 2004. In jedem dieser jährlichen Datensätze sind noch weitere Zählerstände vorhanden, die aber hier
nicht zur Verarbeitung kommen.
Die PV-Anlage hat eine Leistung von 2,5 KW_peak. Die Anlage hat keinen Solarspeicher,
der gesamte PV-Strom wird ins Netz eingespeist.
Mit den Datensätzen dieser PV-Anlage können jetzt Solar-Speicheranlagen berechnet werden. Dabei könne die vorhandenen
Datensätze auch extrapoliert werden. Es kann eine
Speichergrösse vorgegeben werden; das Programm rechnet dann, wie weit der Solar erzeugte Strom im Haus
selbst genutzt werden kann, und welcher Energie-Betrag darüber hinaus noch ins Netz eingespeist werden
kann, bzw. wieviel Strom aus dem Netz bezogen werden muss, wenn der Speicher zu klein ist, oder, wennn er erschöpft ist.
Aus den errechneten Werten ergibt sich der Deckungsgrad der PV-Stromnutzung bezogen auf den gesamten
Stromverbrauch des Hauses in der 365 Tage währenden Abrechnungsperiode.
1. Die Dateneingabe für den Speicher besteht aus 1 Zeile mit den folgenden 6 Werten:
SPMAX=350. SPMIN=5. PVSPE0= 0. ETAlad=90. ETAent=90. STRTAR= 0.27
In dieser Zeile bedeuten:
SPEMAX -- maximale Speicherkapazitaet in KWH
SPEMIN -- minimal zu entladende Speicherkapazitaet in KWH
PVSPE0 -- Speicherladung bei Beginn der Rechnung in KWH
ETALAD -- Wirkungsgrad des Speichers beim Laden in %
ETAENT -- Wirkungsgrad des Speichers beim Entladen in %
STRTAR -- Stromtarif für die Kostenberechnung des PV Gewinn in €/KWH
2. der Datensatz der täglichen PV-Einstrahlung und des täglichen Stromverbrauchs
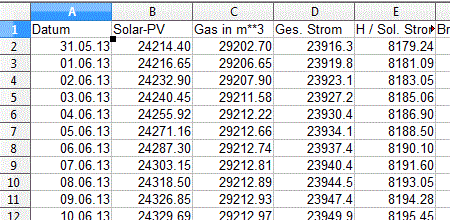
In diesem Ausschnitt vom Datensatz sind noch weitere Zählerstände vorhanden, die jedoch für diesen Bericht keine Bedeutung haben. Hier werden nur das "Datum", die Einträge für den Solarstromzähler: "Solar-PV" und den Hausstromzähler: "Ges. Strom" gebraucht.
Mit dem Datensatz und den Angaben für den Speicher wird folgendes Diagramm berechnet:
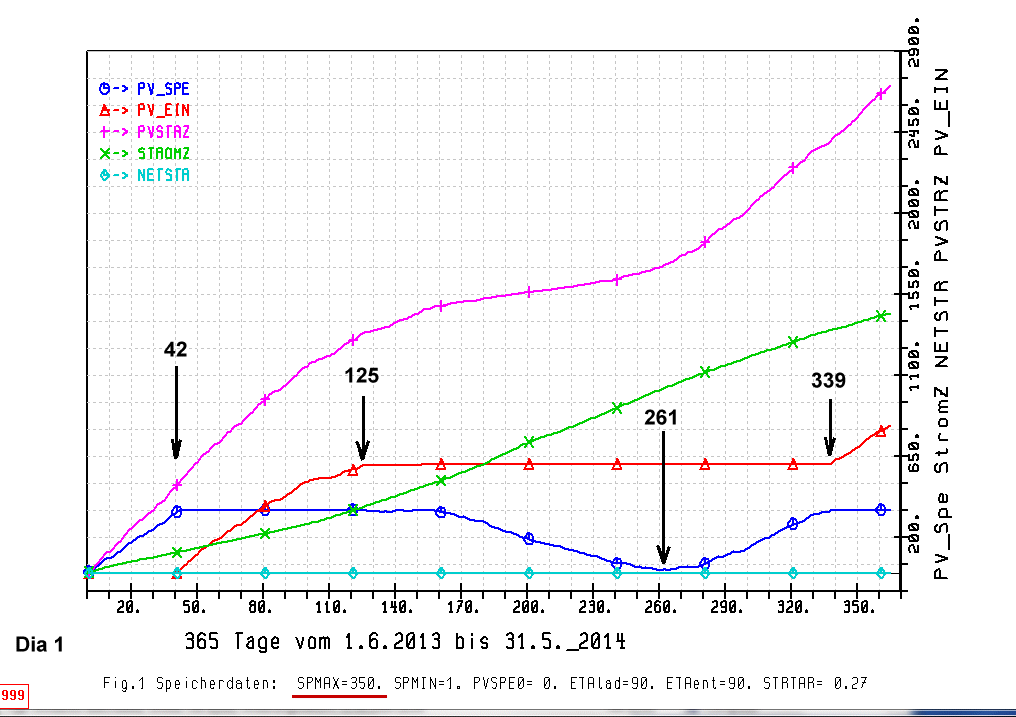
die 5 Variablen in obigem Diagramm bedeuten
PV_SPE Füllstand des Stromspeichers bis maximal SPEMAX, minimal bis SPEMIN in KWH
PV_Ein Zählerstand: ins Netz eingespeister PV_Strom
in KWH
PVStrZ PV-Stromzähler; -aufsummierter täglicher PV_Einspeisegewinn
in KWH
StromZ Stromzähler; Gesamtstromverbrauch im Haus
in KWH
NETSTR aus dem Netz zu beziehender Strom, wenn der Speicher erschöpft ist in KWH
Analysieren wir dieses Diagramm:
In den ersten 42 Tagen ist der PV-Gewinn so hoch, dass der Hausstromverbrauch StromZ komplett davon
gedeckt ist; und der Solarspeicher zusätzlich bis zu seinem maximalen Füllstand von 350 KWH aufgeladen werden kann.
Am 42. Tag ist der Speicher voll. Siehe die Kurve PV_SPE.
Es braucht kein Strom aus dem Netz bezogen werden. Nur am 1. Tag ist hier der PV-Stromgewinn (2,25 KWH) etwas kleiner als der
Stromverbrauch (3,5 KWH);
NETSTR = 1,25 KWH, das ist praktisch = 0
Ab dem 42. bis zum 125. Tag wird der überflüssige PV-Strom auch noch ins Netz eingespeist.
Ab dem 125. Tag reicht der PV-Gewinn nicht mehr aus für den Hausstrombedarf; der Speicher wird jetzt angezapft. Die Energie
aus dem Speicher reicht aber immer noch aus, um den Hausstrombedarf zu decken. Am 261. Tag ist ein Minimum des
Speicherfüllstandes erreicht.
Ab diesem Tag ist der tägliche PV-Gewinn wieder grösser als der Hausstrombedarf, und der Speicher wird von dem
Überschuss wieder aufgeladen.
Am 339. Tag ist der Speicher wieder voll, und der PV- Überschuss wird wieder ins Netz eingespeist.
Bei diesem grossen Speicher braucht kein Strom aus dem Netz bezogen werden. Die Kurve NETSTR bleibt konstant bei 0 (eigentlich 1,25) während des ganzen Zeitraums von 365 Tagen. Wenn der Speicher mit einer Anfangsladung versehen worden wäre siehe Eingabeparameter, dann würde NETSTR konstant bei 0 bleiben.
Im folgendem Diagramm ist mit einem Speicher von 50 KWH gerechnet worden. PV-Modulfläche und Haus-Stromverbrauch wie im vorherigen Diagramm.
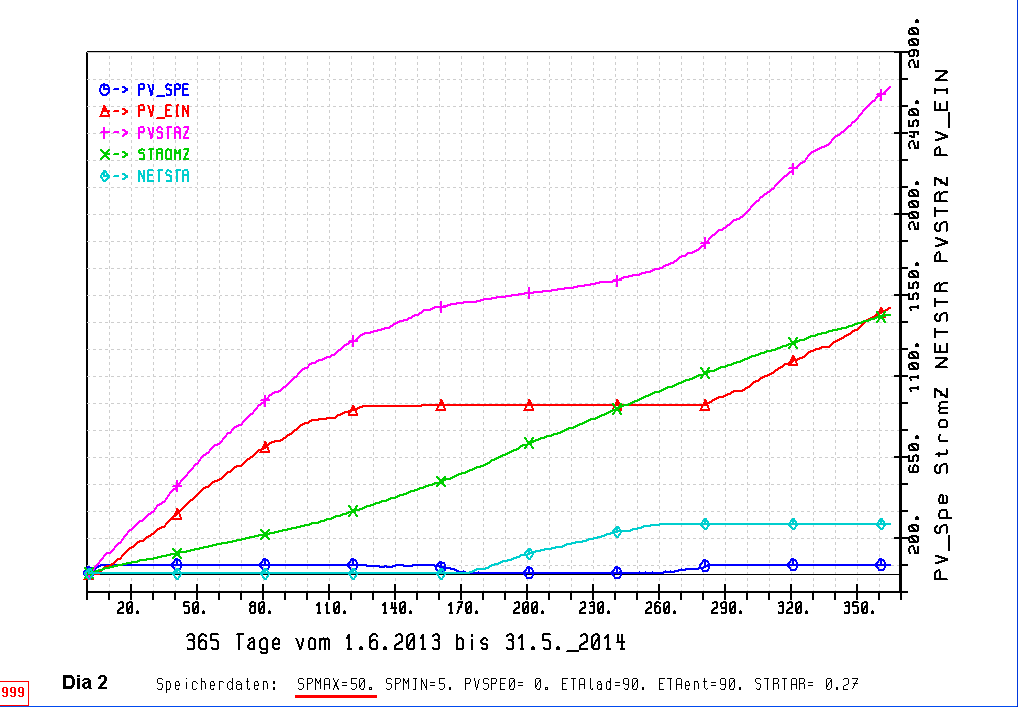
Der solare Deckungsgrad in % errechnet sich zu: 100 * (STROMZ - NETSTR) / STROMZ
In Worten: Deckungsgrad in % = 100 * (Gesamt Stromverbrauch - Strom aus dem Netz) / Gesamt Stromverbrauch
In Zahlen: Deckungsgrad = 100 * (1441,6 - 276,54) / 1441,6 = 80,8 %
Im Diagramm: Dia1 siehe oben mit dem grossen Speicher von 350 KWH ist der Deckungsgrad nahe zu 100%
In Zahlen: Deckungsgrad = 100 * (1441,6 - 1,25) / 1441,6 = 99,9 %
Der geringe Netzstrom Anteil von 1,25 KWH -siehe auch oben- ergibt sich aus der Differenz vom Stromverbrauch von 3,5 KWH an diesem 1. Tag der Rechnung und dem geringeren PV Gewinn an diesem Tag mit 2,25 HWH. An allen weiteren Tagen kann der Hausstromverbrauch immer aus dem Speicher erfolgen.
Deckungsgrad 92,8 % bei doppelter PV-Modulfläche
Im folgendem Diagramm ist bei gleichem Speicher von 50 KWH jedoch mit doppelter PV-Modulfläche gerechnet
worden. Jetzt erreicht der PV-Strom Jahresdeckungsgrad 93 %.
Der tägliche PV Energieertrag ist in dieser Rechnung einfach gleich dem doppelten Energieertrag aus dem
eigenen Datensatz gesetzt worden. Diese Vorgehensweise ist durchaus korrekt
Wegen des nunmehr deutlich höheren Energieertrages sind die Variablen PV_EIN
und PVSTRZ in einem grösseren Massstab aufgetragen; siehe dafür die
linke Ordinate.
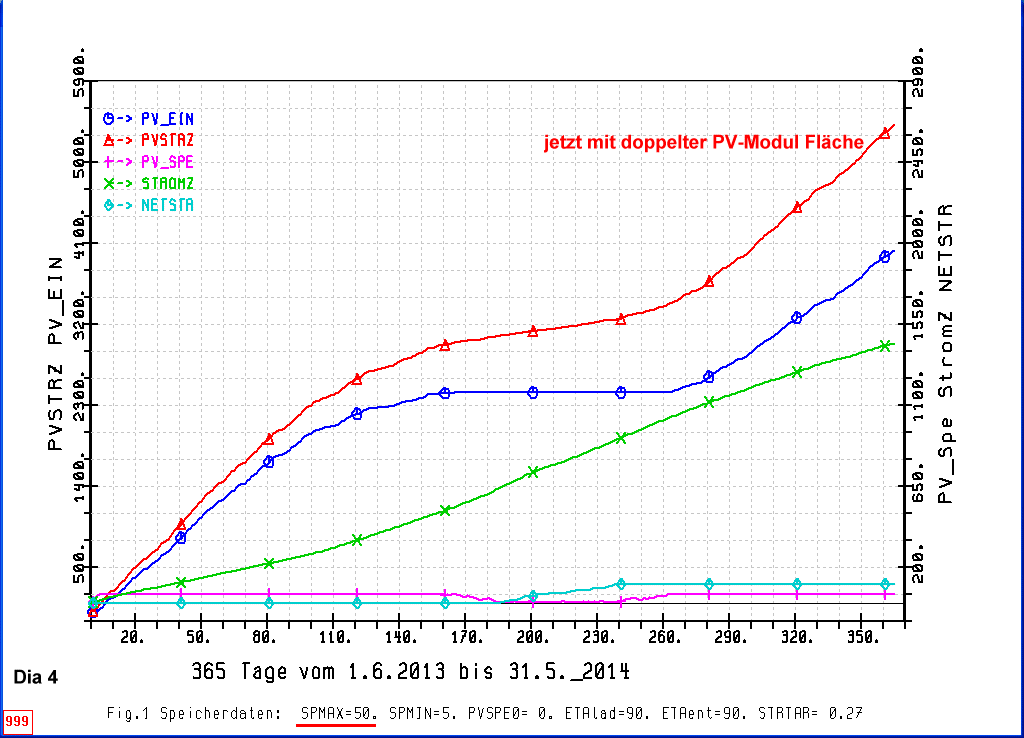
Der solare Deckungsgrad errechnet sich zu: 100 * (1441,6 - 103,87) / 1441,6 = 92,8 %
In diesem Fall, dass die PV-Modulfläche doppelt so gross ist, wie in der vorigen Rechnung, genügt
ein sogar ein wesentlich kleinerer Speicher, um einen recht hohen Deckungsgrad zu erreichen. Der Speicher muss
dann gerade die maximalen täglichen Stromverbräche aufnehmen können.
Eine diesbezügliche Rechnung mit einem Speicher von 5 KWH ergibt immer hin noch einen Jahresdeckungsgrad
von 87 %.
Rechnung mit doppelter PV-Modulfläche und doppeltem Stromverbrauch
Das nächste Diagramm Dia 5 zeigt eine weitere Rechnung mit doppelter PV-Modulfläche und doppeltem
Stromverbrauch und mit einem 50 KWH Speicher.
Im Dia 5 ist auch der tägliche PV-Gewinn und auch der tägliche Stromverbrauch aufgetragen.
Der Jahresdeckungsgrad beträgt hier 59 %
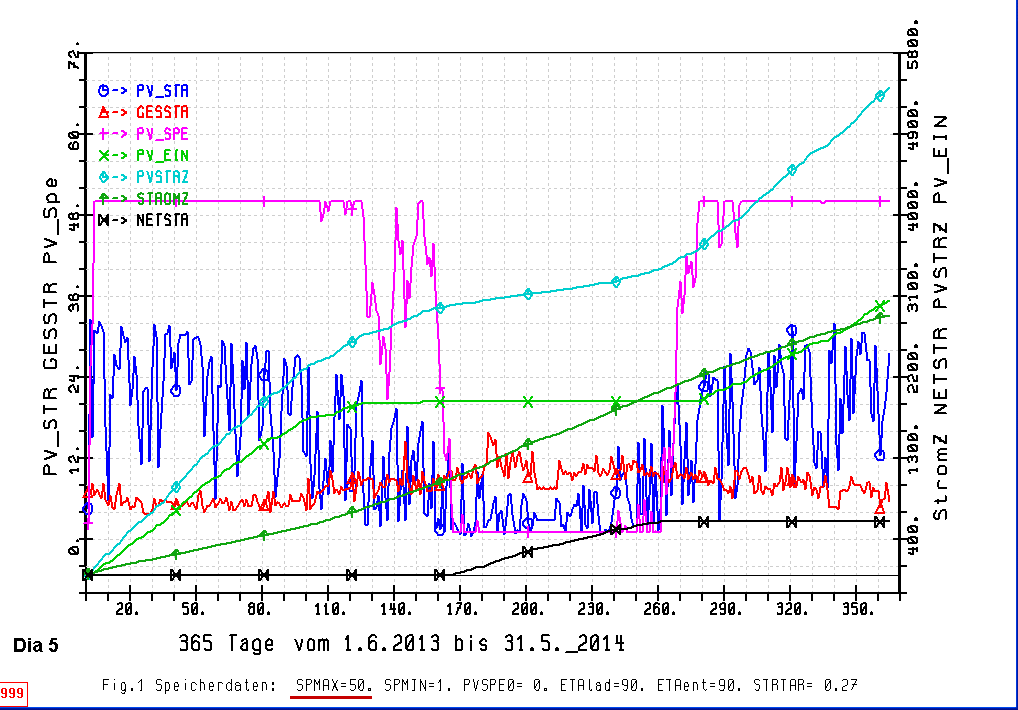
Ein 100% solare Deckungsgrad ist nur mit einem sehr großen Speicher zu realisieren. Wenn der jährliche
Ertrag der PV-Module um ca 80% höher ist als der jährliche Stromverbrauch kann mit einem 50 KWH grossem
Speicher immerhin ein Jahresdeckungsgrad von ca 80 % erreicht werden.
Ist jedoch der jährliche Ertrag der PV-Module ca 2,5 mal so gross wie der jährliche Stromverbrauch
kann mit einem relativ kleinen Sromspeicher ein Jahresdeckungsgrad von > 80 % gerechnet werden. Ein solcher Speicher
muss geringfügig grösser sein als der grösste Tagesstromverbrauch.
Wenn Sie möchten, geben Sie mir bitte einen Kommentar per
e-mail.
Meine e-mail Adresse: