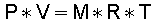
2. Zustandsänderungen der Gase
2.1 Die isotherme Zustandsänderung
2.2 Die isobare Zustandsänderung
2.3 Die isochore Zustandsänderung
2.4 Adiabatische und polytrope Zustandsänderungen
3. Der ideale Stirling Prozeß und der Carnot Prozeß im P-V und T-S Diagramm
3.1 Der isotherme Stirling Prozeß in einer Maschine mit Kurbeltrieb
Im vorigen Kapitel habe ich versucht, die Arbeitsweise des Stirlingmotors "logisch" zu erklären. Das kleine Gedankenexperiment, Erhitzung und Abkühlung von Luft, die in einer Blechdose -mit Gummihaut als Deckel- eingeschlossen war, diente dazu, die "Zustandsgleichung idealer Gase"
(1)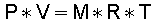
(manchmal auch in sprachlich laxer Weise als das "ideale Gasgesetz" bezeichnet)
anschaulich zu machen. An dieser Stelle
möchte ich -insbesondere für Studenten des Maschinenbaues- den
Arbeitsprozeß des Stirlingmotors aus thermodynamischer Sicht darstellen.
Wir werden sehen, daß wir dazu neben der "Zustandsgleichung idealer Gase" auch den
1. und 2. Hauptsatz der Thermodynamik anwenden müssen siehe |1| und
|2|. Die verschiedenen Ausführungsformen des Stirlingmotors - a
, b , g , Ringboom
Typ, Wasserkolben sog. Fluidyne, oder Freikolben Stirlingmotoren sollen hier nur beiläufig
betrachtet werden, da der thermodynamische Prozeß bei allen diesen Ausführungsarten
immer der gleiche ist.
Durch die Art der Kinematik von Kolben- und Verdrängerbewegung kann jedoch der
Prozeßverlauf beeinflußt werden, was sich in unterschiedlich ausgeformten Kurven
im P-V und T-S Diagramm zeigt.
Dieser Bericht erhebt nicht den Anspruch, vollständige Berechnungshilfen zu geben. So wird
z.B. der Wärmeübergang in Erhitzer, Kühler und Regenerator nicht behandelt; siehe
dazu jedoch |7| , |13| und |5|.
Dafür werden hier Einzelheiten besprochen, die speziell den auf dieser Homepage vorgestellten
2 mal doppelt wirkenden Stirlingmotor betreffen. Siehe den Bericht dazu.
Es werden Kenntnisse in Thermodynamik und höherer Mathematik vorausgesetzt.
Es ist üblich, daß man zunächst einmal Annahmen und Voraussetzungen definiert auf die die nachfolgenden Erklärungen fußen werden:
Bei jeder Umdrehung der Kurbelwelle wird immer die gleiche Nutzarbeit verrichtet. (Achtung: Dies bedeutet nicht, daß das Drehmoment als Funktion des Kurbelwinkels konstant ist!)
Jede Umdrehung erfolgt in der gleichen Zeit wie die vorhergehende Umdrehung. (Achtung: Dies bedeutet nicht notwendigerweise, daß die Winkelgeschwindigkeit der Kurbelwelle an allen Winkelpositionen konstant ist!)
Im Motor befindet sich immer eine konstante Gasmasse. Leckverluste gibt es nicht.
Diese konstante Gasmasse erfährt während einer Umdrehung in den verschiedenen Regionen des Motors unterschiedliche Zustandsänderungen. Jedoch bei einer bestimmten Kurbelwinkelstellung herrscht immer wieder der gleiche Zustand bezüglich der Druck- und Temperaturverteilung, wie er während der vorhergehenden Umdrehung bei dieser Kurbelwinkelstellung auch bestand. Diese Annahme ist die Definition für den thermodynamischen Kreisprozeß.
Anders ausgedrückt: Ein thermodynamischer Kreisprozeß ist ein geschlossener Prozeß, der periodisch wiederkehrend mit ein und derselben Arbeitsfluidmasse abläuft (im Stirlingmotor ist dieses Arbeitsfluid ein Gas) , bei dem man nur dafür sorgt, daß am Ende jeder Periode der Anfangszustand wieder erreicht wird. Das kann man erreichen, wenn die Zustandsänderungen in diesem Kreisprozeß umkehrbar sind.
Arbeitsprozesse stellt man anschaulicherweise gern im P-V Diagramm dar; siehe Fig. 1. Wenden wir auf diesen Prozeß den 1. Hauptsatz der Thermodynamik an, den Satz von der Erhaltung der Energie:
Die einem Arbeitsgas übertragene Energie "Q" kann teils in Ausdehnungsarbeit und teils in Änderung der inneren Energie "U" des Arbeitsgases umgesetzt werden.
In Differentialform geschrieben lautet der 1 Hauptsatz:
(2)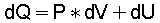
Da die innere Energie "U" eines Gases nur von seiner Temperatur "T" abhängig ist , gilt unter der Annahme, daß die spez. Wärme "cv" in dem betrachteteten Temperaturbereich konstant ist:
(3)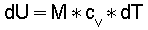 "M" ist die Masse des Gases.
"M" ist die Masse des Gases.
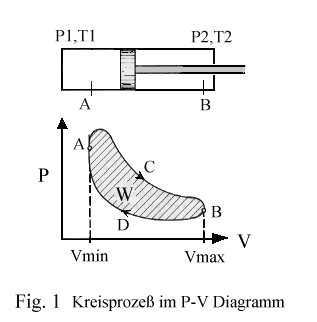 Ausgangszustand in dem Kreisprozeß
in Fig. 1 sei der Punkt "A" Hier sei der Gasdruck "P1" , die Gastemperatur
sei "T1", die innere Energie des Gases sei hier "U1". Punkt "B"
sei der Endzustand der Kolbenbewegung. Hier herrschen der Druck "P2", die Temperatur
"T2" und die innere Energie "U2". Die Punkte "A" und "B",
in denen die Bewegungsrichtung des Kolbens umkehrt, heißen die "Totpunkte".
Die Fläche unter der Linie "Vmin - A - C - B - Vmax
" bildet die nach außen abgegebene Ausdehnungsarbeit als Folge der
dem Prozeß zugeführten Energie "Q1". Der Pfeil bei "C" markiert
die Richtung der Arbeitsabgabe. Nach dem 1. Hauptsatz -siehe Gl (2)
- errechnet sich "Q1" zu:
Ausgangszustand in dem Kreisprozeß
in Fig. 1 sei der Punkt "A" Hier sei der Gasdruck "P1" , die Gastemperatur
sei "T1", die innere Energie des Gases sei hier "U1". Punkt "B"
sei der Endzustand der Kolbenbewegung. Hier herrschen der Druck "P2", die Temperatur
"T2" und die innere Energie "U2". Die Punkte "A" und "B",
in denen die Bewegungsrichtung des Kolbens umkehrt, heißen die "Totpunkte".
Die Fläche unter der Linie "Vmin - A - C - B - Vmax
" bildet die nach außen abgegebene Ausdehnungsarbeit als Folge der
dem Prozeß zugeführten Energie "Q1". Der Pfeil bei "C" markiert
die Richtung der Arbeitsabgabe. Nach dem 1. Hauptsatz -siehe Gl (2)
- errechnet sich "Q1" zu:
(4)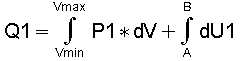
"Q1" beinhaltet also die Arbeitsabgabe und die Änderung der inneren Energie DU1. Damit dieser Prozeß wieder seinen Ausgangszustand "A" erreichen kann, muß der Kolben zurückbewegt und dafür muß Arbeit aufgewendet werden. Dieser Arbeitsaufwand verläuft längs der Linie "Vmax - B - D - A - Vmin. Da die Temperatur "T2" im Punkt "B" mit Sicherheit nicht dieselbe ist wie "T1" im Punkt "A". muß ebenfalls -parallel zu dem Arbeitsaufwand- auch die innere Energie von "U2" bei Punkt "B" auf "U1" bei Punkt "A" geändert werden; Insgesamt ist der Aufwand "Q2" nötig, um den Zustand "A" wieder zu erreichen:
(5)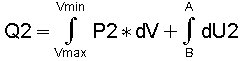
Die Addition beider Energiebeträge Q1 + Q2 ergibt nun die eigentliche Nutzarbeit des Prozesses, die in Fig. 1 als schraffierte Fläche dargerstellt ist.
(6)
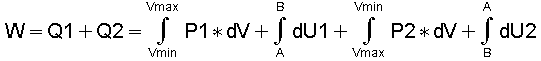
Da gemäß der Voraussetzung für den Kreisprozeß der Anfangszustand gleich dem Endzustand ist, muß für die Änderungen der inneren Energie gelten:
(7)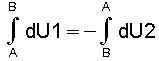 bzw. DU1 = - DU2
bzw. DU1 = - DU2
Betrachten wir die Richtung der Integration in den Ausdrücken für "Q2" , so ist zu erkennen, daß es sich hier -im Gegensatz zu den Ausdrücken in "Q1"- um negative Größen handelt. Nach alter Vereinbarung bilden negative Vorzeichen "abgeführte" Energie, wie "Abnahme" der inneren Energie aber "Zuführung" äußerer Arbeit (z.B. bei der Kompression eines Gases).
Demgegenüber bedeutet ein positives Vorzeichen: "Thermisch zugeführte" Energie, "Zunahme" der inneren Energie und "Abgabe" von Arbeit nach außen.
Um die Zustandsänderungen des Arbeitsfluids im Kreisprozeß soll es in diesem Kapitel gehen. Deren Kenntnis ist eine wichtige Voraussetzung zur Berechnung aller Wärmekraftprozesse. Da uns hier der Stirlingprozeß interessiert, soll im wesentlichen nur auf diesen eingegangen werden. Die im Folgenden diskutierten 4 Zustandsänderungen betreffen eigentlich nur ideale Gase; man kann sie aber mit genügender Genauigkeit auch auf reale Gase wie Luft, Wasserstoff usw. anwenden. Als optimales Arbeitsgas für den Stirlingmotor gilt das Edelgas Helium. Mit Helium hätten wir sogar ein ideales Gas, für welches die "Zustandsgleichung idealer Gase" und die zu besprechenden Zustandsänderungen genau zutreffen.
2.1 Die isotherme Zustandsänderung
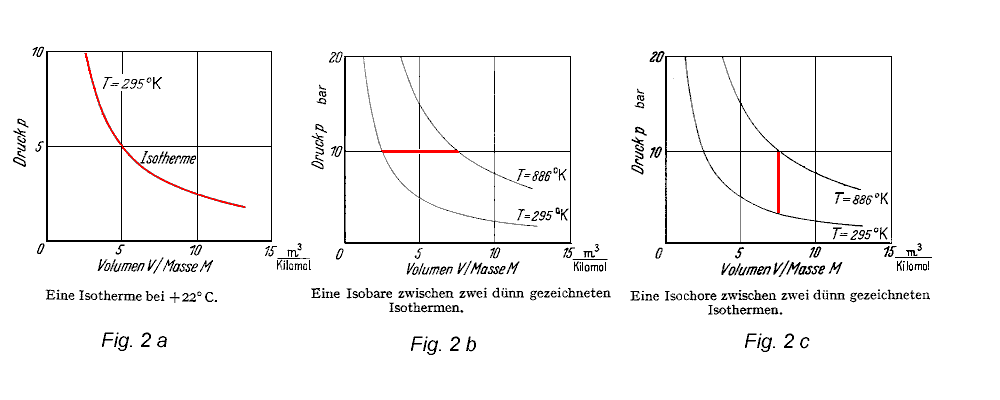
Fig. 2a zeigt die "Isotherme", also eine Linie gleicher Temperatur; sie bildet im P-V Diagramm eine Hyperbel. Betrachten wir mit dem 1. Hauptsatz einen isothermen Wärmekraftprozeß nach Gl (2), so entfällt der Term "dU", da ja wegen der gleichbleibenden Temperatur keine Änderung der inneren Energie stattfindet. Der 1. Hauptsatz angewendet auf die isotherme Zustandsänderung lautet also:
(8)
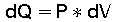
oder, wenn "P" mit der "Zustandsgleichung idealer Gase" ersetzt wird zu: P = M * R * T / V ergibt sich aus Gl (8):
(9)
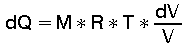
Diese Differentialgleichung (9) läßt sich sehr einfach integrieren. Wir erhalten dann für den isothermen Prozeß die Ausdehnungsarbeit von Vmin bis Vmax :
(10)
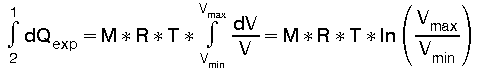
Das bedeutet: Die in einen isothermen Prozeß auf eine Gasmenge mit der Masse M hineingesteckte Wärmeenergie kann 100% in Ausdehnungsarbeit umgesetzt werden!!
Für eine Kompressionsarbeit von Vmax - Vmin ergibt sich:
(11)
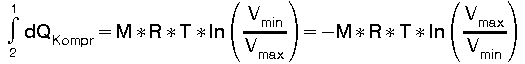
Bei der isothermen Kompression wird also die aufgewendete Energie 100% in Kompressionsarbeit umgesetzt.
Leider ist die isotherme Zustandsänderung für technische Wärmekraftprozesse nicht zu erreichen; denn die isotherme Zustandsänderung erfordert unendliche Zeit für den Wärmeübergang mit DT = 0. Fälschlicherweise bringt man den Stirlingprozeß immer mit isothermen Zustandsänderungen in Zusammenhang. Hierbei verwechselt man jedoch den idealen Stirlingprozeß mit dem technisch nur möglichen realen Stirlingprozeß. Wir werden dies im nächsten Kapitel näher besprechen.
2.2 Die isobare Zustandsänderung
Fig. 2b zeigt die "isobare" Zustandsänderung. Sie erfolgt bei konstant gehaltenem Druck. Nach der "Zustandsgleichung idealer Gase" lautet die Gleichung der Isobaren:
(12)
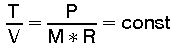
Das bedeutet, das Volumen wächst proportional der Temperatur. Die Ausdehnungsarbeit in den Grenzen von Vmin bis Vmax errechnet sich zu:
(13)
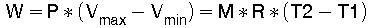
wobei T2 die Temperatur des Gases an der Stelle Vmax ist, T1 ist die Temperatur an der Stelle Vmin .
Da T2 > T1 ist, erhöht sich bei isobarer Ausdehnung auf dem Weg von Vmin bis Vmax die innere Energie. Gem. Gl (2) ist dem isobaren Prozess die Energie "Q" zuzuführen:
(14)
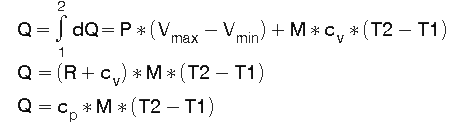
Die Gaskonstante ist R = cp - cv . Das Verhältnis der spez. Wärmen ist k = cp / cv . Das Verhältnis von abgeführter Ausdehnungsarbeit "W" zu zugeführter Wärmeenergie "Q" ist:
(15)
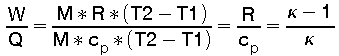
Ein Rechenbeispiel: Für Helium als Arbeitsgas mit k = 1.66 ist das Verhältnis W/Q = 0.39 . Also nur 39 % der zugeführten Wärmeenergie wird beim isobaren Prozeß in Ausdehnungsarbeit umgesetzt !!!
2.3 Die isochore Zustandsänderung
Fig. 2c zeigt die "isochore" Zustandsänderung; diese erfolgt bei konstant gehaltenem Volumen. Ihre Gleichung lautet:
(16)
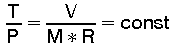
Druck und Temperatur sind bei der isochoren Zustandsänderung einander proportional. Es erfolgt keine Ausdehnungsarbeit; denn das Volumen bleibt ja konstant. Die thermisch zugeführte Energie wird restlost zur Erhöhung der inneren Energie DU umgesetzt.
(17)
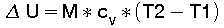
Die isochore Zustandsänderung wäre wünschenswert im Wärmekraftprozeß. Doch auch sie ist in einer kontinuierlich sich drehenden Maschine nicht zu realisieren, da sie Zeit erfordert während das Volumen in dieser Zeitspanne konstant bleiben muß, würden die Massenkräfte unendlich groß. Es gibt aber einige technische Vorrichtungen in Stirlingmotoren, die eine isochore Zustandsänderung annähern. Die ist z.B. die Verdrängersteuerung nach Ringbom: Ein sehr leichter Verdränger wird hier völlig unabhängig von der Kurbelwelle durch eine Art Kippschwingung rasch diskontinuierlich bewegt. Diese diskontinuierliche Bewegung wird ausgelöst, wenn ein bestimmter Gasdruck überschritten oder unterschritten wird. Eine gute Beschreibung der Ringbomsteuerung zeigt Senft in |6|
2.4 Adiabatische und polytrope Zustandsänderungen
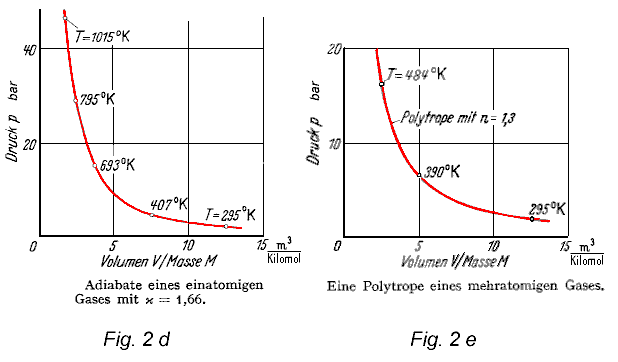
Fig. 2d zeigt die "adiabatische" Zustandsänderung. Sie erfolgt ohne thermischen Energieaustausch mit der Umgebung. Hier ist also Q = 0 und dQ = 0. Dennoch kann wie aus Fig. 2d ersichtlich Ausdehnungsarbeit verrichtet werden. Dies erfolgt auf Kosten der inneren Energie des Arbeitsgases. Der Gasdruck sinkt nicht nur infolge der Volumenzunahme, sondern gleichzeitig wegen der damit verbundenen Abkühlung. Wenden wir den 1. Hauptsatz auf die adiabatische Zustandsänderung an:
(18)
Daraus gewinnt man nach einigen Rechenschritten -siehe |2|- die Gleichung für die Adiabate:
(19)
 k ist der "Adiabatenexponent",
k = cp / cv .
k ist der "Adiabatenexponent",
k = cp / cv .
Die Adiabate ist eine steilere Kurve als die Isotherme im P-V Diagramm: Die differentielle Druckänderung ist bei der Adiabaten "k" mal so groß wie bei der Isothermen. Der Adiabaten kommt eine große Bedeutung zu bei der theoretischen Erfassung des Dampf- und Gasturbinenprozesses.
Da es auch bei guter Isolierung in Wärmekraftmaschinen praktisch nicht möglich ist, adiabatische Zustandsänderungen in Gasen ohne Wärmeaustausch mit den Wandungen zu erreichen -also wirklich bei Q = 0-, hat die Adiabate mehr theoretische als praktische Bedeutung. Sie wird bei der Berechnung von Wärmekraftprozessen ersetzt durch die "polytrope" Zustandsänderung. Die polytrope Zustandsänderung erfolgt -siehe Fig.2e- bei einer für die adiabatische Zustandsänderung nicht ausreichenden Wärmeisolation. Der Druck sinkt bei der polytropen Expansion etwas geringer als er es bei der adiabatischen Expansion tun würde. Das bedeutet, daß die Abkühlung hier wegen der unzureichenden Wärmeisolation nicht so stark ausfällt. Die Gleichung der Polytropen lautet:
(20)
 mit dem Polytropenexponenten n < k,
mit dem Polytropenexponenten n < k,
P1 ist der Gasdruck beim Volumen Vmin, P2 der Gasdruck beim Volumen Vmax
Mit Gl (20) und der "Zustandsgleichung idealer Gase" Gl (1) erhält man die nützlichen Beziehungen:
(21)
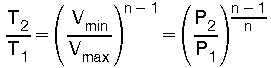
Die Ausdehnungsarbeit längs der polytropen Zustandsänderung ist:
(22)
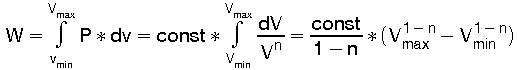
Mit Gl (20) und der "Zustandsgleichung idealer Gase" Gl (1) erhält man aus Gl (22)
(23)
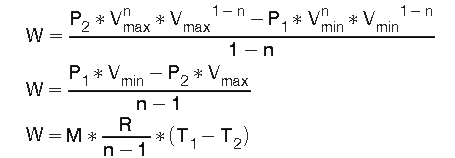
Für die adiabatischen Zustandsänderungen ist in den Gl (20) bis (23) n = k = cp / cv zu setzen. Es errechnet sich dann bei der adiabatischen Ausdehnung nach Gl (23) die nach außen abgegebene Arbeit:
(24)
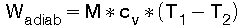
3. Der ideale Stirlingprozeß und der Carnot Prozeß im P-V und T-S Diagramm
Um den Stirlingprozeß zu erklären, ist es sinnvoll, ihn zunächst in seiner idealisierten Form zu betrachten.
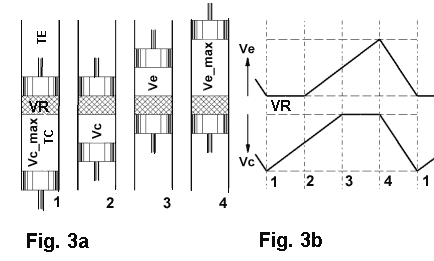
Stellen wir uns einen idealen Stirlingmotor vor als einen Zylinder, in dessen Mitte
ein Regenerator VR sitzt Fig.3a. Zu beiden Seiten dieses Regenerators befindet sich je ein beweglicher Kolben.
Wir werden den Regenerator in Kapitel 5 genauer besprechen. Zwischen den beiden Kolben
ist eine Gasmasse "M" eingeschlossen. Oberhalb des Regenerators herrscht die
heiße Temperatur TE, unterhalb die kalte Temperatur TC. Nun definieren wir
einen Startpunkt "1". Siehe Fig. 3a -1- von dem aus wir 4 verschiedene
Kolbenstellungen beobachten wollen. Die Volumina in den Räumen dieser Maschine sind
entsprechend den Stellungen der Kolben in Fig. 3b aufgetragen.
Alles Gas befindet sich bei maximalem Volumen Vc_max im kalten Bereich des Motors und hat die Temperatur TC angenommen. Der Druck des Gases sei hier P1. Der untere Kolben hat seine tiefste Position. Der obere Kolben liegt dicht am Regenerator, sodaß sich kein Gas im heißen Bereich befindet; Ve=0.
Der obere Kolben ist in seiner Position geblieben Ve = 0. Der untere Kolben hat bei der konstanten Temperatur TC das Gas verdichtet auf Vc. Das ist der Zustand gem. Fig. 3a -2-. Der Druck ist dabei auf P2 angestiegen. Isotherme Kompression von -1- nach -2-.
Der untere und der obere Kolben bewegen sich gleichmäßig und gleichzeitig und legen den gleichen Weg zurück. So gelangt das Gas bei isochorer Zustandsänderung -also bei gleichem Volumen- durch den Regenerator in den heißen Bereich -jetzt Ve- und nimmt dabei die dort herrschende Temperatur TE an. Fig. 3a -3-. Der Druck erhöht sich entsprechend auf P3. Der untere Kolben hat seine oberste Position erreicht; jetzt ist kein Gas mehr im kalten Bereich. Vc = 0. Isochore Wärmezufuhr von -2- nach -3-.
Der untere Kolben verbleibt in dieser OT - Stellung Vc = 0. Der obere Kolben bewegt sich weiter bis zu seiner Endstellung. Fig. 3a -4-. Dabei dehnt sich das Gas isotherm aus und erreicht ein Maximum im heißen Bereich: Ve_max. Der Druck ist dabei auf "P4" gesunken. Isotherme Expansion von -3- nach -4-.
Damit der Ausgangszustand Fig. 3a -1- wieder erreicht wird, muß das Gas durch gleichzeitige und gleichmäßige Bewegung beider Kolben jetzt isochor unter Wärmeentzug durch den Regenerator in den kalten Bereich gelangen.
Eigendlich müßten diese 4 idealen Zustandsänderungen, gemäß dem was in Kapitel 2.1 und 2.3 gesagt wurde, unendlich langsam erfolgen. Wir machen aber keinen großen Fehler, wenn wir sagen, daß diese Zustandsänderungen in 4 gleichen Zeitabschnitten erfolgen. Dann können wir die dabei entstehenden Volumenänderungen in "Ve" und "Vc" gem. Fig. 3b auftragen. Ein komplettes P-V Diagramm dieses idealen Stirlingprozesses zeigt Fig. 3. Die Endpunkte der oben beschriebenen Zustandsänderungen 1 -2 -3 -4 sind in diesem P-V Diagramm mit eingetragen.
Wir halten fest: Der ideale Stirlingprozeß beteht aus 4 reinen Zustandsänderungen
gem. Fig. 3, die bei diskontinuierlicher Kolbenbewegung nacheinander
ablaufen:
Von 1 bis 2
verläuft eine isotherme Kompression bei der Temperatur "TC" ;
von 2 bis 3 folgt eine isochore Wärmezufuhr von "TC"
auf "TE"; dann folgt
von 3 bis
4 eine isotherme Expansion bei der Temperatur "TE" und danach
von
4 bis 1 ein isochorer Wärmeentzug, womit der hier willkürlich
gewählte Ausgangszustand 1 bei der Temperatur "TC" wieder erreicht ist.
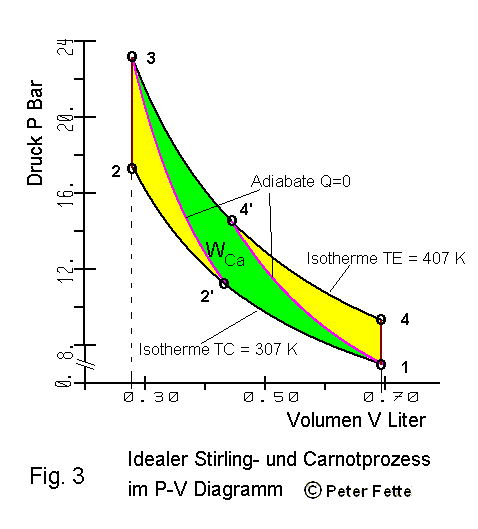
Die isotherme Kompressionsarbeit WKomp kann mit Gl (11) errechnet werden. Das Volumen der Isochoren 4 - 1 von ca. 0.69 Liter ist in Gl (11) als Vmax und das Volumen der Isochoren 2 - 3 ca. 0.28 Liter ist als Vmin einzusetzen. Die Expansionarbeit WExp auf der Isothermen von 3 nach 4 wird gem. Gl (10) errechnet. Da während der isochoren Zustandsänderungen keine Ausdehnugsarbeit anfällt, ergibt sich die Nutzarbeit dieses idealen Prozesses zwischen 2 Isothermen zu: WNutz = WExp + WKomp. Dieser Nutzarbeit WNutz entspricht die Fläche im P-V Diagramm Fig. 3, die durch die Linien 1 - 2 - 3 - 4 - 1 eingeschlossen wird.
(25) 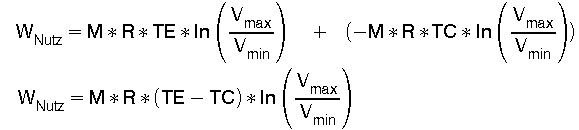
Während der isochoren Zustandsänderung von 2 bis 3 muß Energie zugeführt werden. Diese zuzuführende Energie dient ausschließlich der Erhöhung der inneren Energie des Arbeitsfluids von der Temperatur TC auf TE und errechnet sich nach Gl (17) zu:
(26) 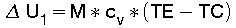
Während der isochoren Zustandsänderung von 4 bis 1 muß Energie abgeführt werden. Diese abzuführende Energie verringert die inneren Energie des Arbeitsfluids von der Temperatur TE auf TC und errechnet sich ebenfalls nach Gl (17) zu:
(27) 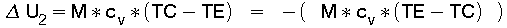
Diese Energiebeträge entsprechen sich: D U1 = - D U2. Sie können im System bleiben, da sie sich gegeneinander aufheben. Man denke sich eine Vorrichtung, die diese Energie zum geeigneten Zeitpunkt aufnimmt und zum anderen Zeitpunkt wieder abgibt. Diese Vorrichtung ist bei der technischen Realisierung eines Stirlingprozesses der Regenerator. Wir werden den Regenerator in nächsten Kapitel besprechen.
Der ideale Stirlingprozess verläuft praktisch unendlich langsam, da beide isotherme Zustandsänderungen sehr viel Zeit brauchen; denn man muß ja dafür sorgen, daß in jedem Augenblick der Zustandsänderung Gleichgewicht herrscht, das heißt, es muß Wärmeaufnahme und Wärmeabgabe bei unendlich kleinen Temperaturunterschieden erfolgen. In Wirklichkeit kann es also keinen idealen Stirlingprozeß geben. Man könnte sich jedoch fragen, ob man die "isothermen" Zustandsänderungen nicht dadurch annähern kann, daß man ein konstantes Temperaturgefälle bei der Energiezufuhr und Kühlung zuläßt und somit auf der Zylinderinnenseite eine konstante Temperatur während der Expansion und Kompression hat. Daß auch dies in praktischen Maschinen nicht vollständig möglich ist, werden wir auch im nächsten Kapitel besprechen.
Es gibt aber noch einen anderen -theoretischen- Prozeß zwischen 2 Isothermen, bei dem ebenfalls nur während dieser isothermen Zustandsänderungen thermische Energie zu- bzw. abgeführt zu werden braucht. Das ist der Carnot Prozeß. Eigentlich ist der Carnot Prozeß eher "erfunden" worden, als der ideale Stirling Prozeß und wir würden ihn auch zuerst besprechen, wenn es sich in diesem Vortrag nicht hauptsächlich um den Stirling Prozeß drehen würde.
Der Carnot Prozeß - er ist ebenfalls in Fig. 3 eingezeichnet- verläuft zwischen 2 isothermen und 2 adiabatischen Zustandsänderungen längs des Linienzuges 1 - 2' - 3 - 4' - 1:
Beginnen wir in der Beschreibung des Carnot Prozesses wie beim idealen Stirling Prozeß beim Ausgangspunkt 1 in Fig. 3. Auch hier erfolgt zunächst die isotherme Kompression; diese jedoch nicht bis zum Volumen Vmin sondern nur bis zum Volumen unter dem Punkt 2'. Ab Punkt 2' beginnt eine adiabatische Kompression bis Vmin erreicht ist in Punkt 3. Die Temperatur des Gases ist infolge dieser adiabatischen Kompression dabei von "TC" auf "TE" angestiegen. Dafür braucht beim Carnotprozeß keine isochore Wärmezufuhr mehr zu erfolgen, die der ideale Stirlingprozeß "kostenlos" aus dem Regenrator bezieht. Der Carnotprozeß kennt keinen Regenerator, weil er auch keinen Regenerator nötig hat. Die Kompressionsarbeit, die längs der Adiabaten von 2' bis 3 verrichtet werden muß, und als mechanische Energie von außen zugeführt werden muß, ist deutlich höher als die Kompressionsarbeit der Isothermen auf dem entsprechenden Teilstück 2' bis 2.
Ab Punkt 3 erfolgt wieder isotherme Ausdehnung jedoch nur bis zum Punkt 4'. Danach setzt eine adiabatische Entspannung ein, bis das Volumen Vmax im Punkt 1 erreicht ist. Die Temperatur des Arbeitsfluids ist dabei von "TE" auf "TC" abgesunken.
Der Nutzarbeit des Carnot Prozesses entspricht im P-V Diagramm Fig. 3 die grün ausgefüllten Fläche 1 - 2' - 3 - 4' - 1. Man erkennt gleich, daß die Nutzarbeit des Carnot Prozesses deutlich geringer ist als die Nutzarbeit des idealen Stirling Prozesses. Woran liegt das? Nun die isotherme Expansion ist dadurch gekennzeichnet, daß zugeführte Wärmeenergie 100% in Ausdehnungsarbeit umgesetzt wird; siehe Gl (10). Der Carnotprozeß nutzt dies nur von 3 bis 4'. Längs der adiabaten Expansion von 4' bis 1 wird keine Energie zugeführt, Q=0 ! Die adiabatische Ausdehnungsarbeit wird auf Kosten der inneren Energie des Arbeitsfluids verrichtet; siehe Gl (24). Es ist also wärend der gesamten Expansion im Carnotprozeß (Linie 3 - 4' - 1) deutlich weniger Energie zugeführt worden als während der isothermen Expansion von 3 - 4 beim idealen Stirlingprozeß. Weiter verringert wird die Nutzarbeit des Carnotprozesses durch Mehraufwand an Kompressionsarbeit, die dem Prozeß ja von außen zugeführt werden muß. Diesem Mehraufwand an adiabatischer Kompressionsarbeit gegenüber der isothermen Kompressionsabeit entspricht die Fläche 2' - 2 - 3 - 2' in Fig. 3.So ergibt sich die Nutzarbeit des Carnotprozesses aus: WNutz = (Wisoth + Wadiab)exp + (Wisoth + Wadiab)komp.
(28)
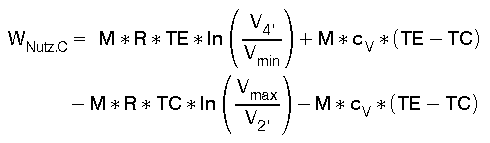
Aus Gl(28) erkennen wir, daß die
adiabatische Expansionsarbeit genau die adiabatische Kompressionsarbeit aufwiegt -siehe dazu die
Gl (24).
Ähnlich wie die Wirkung des Regenerators beim idealen Stirlingprozeß,
muß es beim Carnotprozeß eine Vorrichtung geben, die die adiabatische
Ausdehnungsarbeit zwischenspeichert, um sie zu einem geeigneten späteren
Zeitpunkt restlos in adiabatische Kompressionsarbeit zu überführen.
In technisch realisierten Maschinen kann man diese Vorrichtung mit einem
Schwungrad vergleichen.
Die Volumenverhältnisse in Gl (28) V4'/Vmin und Vmax/V2' sind einander gleich. Das folgt aus der Voraussetzung des geschlossenen Prozesses, den 2 Adiabaten (Q=0) und 2 Isothermen des Carnotprozesses bilden. Die Ableitung dafür folgt nach |7|:
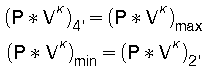
schreiben wir für Vk = V * V(k-1) und dividieren beide Gleichungen durch einander dann ergibt sich:
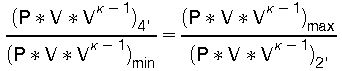
Da die Temperatur an der Stelle 3 = Vmin die gleiche ist wie an der Stelle 4' nämlich TE und ebenso die gleiche Temperatur TC an der Stelle 2' wie an der Stelle 1 = Vmax herrscht, ist nach der "Zustandsgleichung idealer Gase":
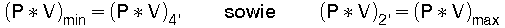
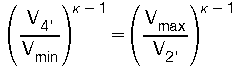
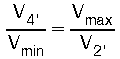 Damit wird jetzt aus Gl (28)
Damit wird jetzt aus Gl (28)
(29) 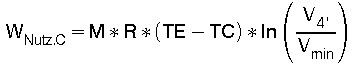
Das P-V Diagramm ist besonders gut geeignet, Ausdehnungsarbeiten als Flächen zu zeigen,
wärend das T-S Diagramm dazu dient, Energiebeträge als Flächen darzustellen.
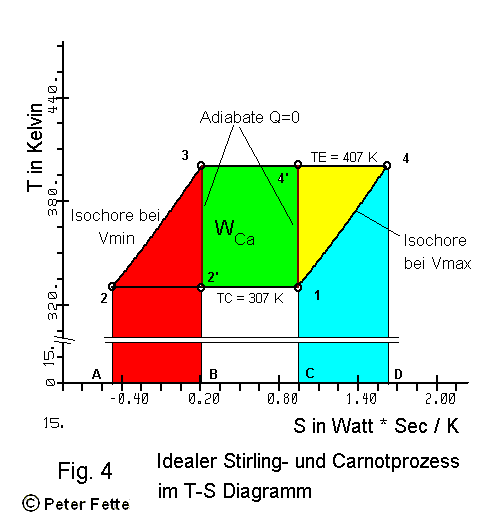
Im T-S Diagramm werden die isochoren Energiebeträge sichtbar. Während die Isochoren im P-V Diagramm vertikale Linien sind siehe Fig. 3, werden sie im T-S Diagramm als geneigte Kurvenzüge dargestellt. In Fig. 4 sind die Isochoren wegen der relativ geringen Temperaturdifferenz TE-TC nur als kurze Kurvensegmente sichtbar, die eher als gerade Linien auffallen. Die hellblau unterlegte Fläche, die eingeschlossen wird durch 4 - 1 - C - D - 4 entspricht dem isochoren Wärmeentzug bei Vmax siehe Gl (27). Und die rot unterlegte Fläche, die durch 2 - 3 - B - A - 2 eingeschlossen wird entspricht der isochoren Wärmezufuhr bei Vmin siehe siehe Gl (26). Diese beiden Flächen sind also auch gleich groß. Die Energiebeträge, die diesen beiden Flächen entsprechen, werden im idealen Stirlingprozeß bei Vmax vollständig vom Regenerator aufgenommen, und bei Vmin vollständig wieder an das Arbeitsfluid abgegeben. Die Nutzarbeit des idealen Stirlingprozesses wird dargestellt durch die Fläche 1 - 2 - 3 - 4 - 1.
Im T-S Diagramm sind adiabatische Zustandsänderungen als vertikale Linien dargestellt, die oben und unten durch die entsprechenden Isothermen begrenzt sind, siehe die Linien 2' - 3 und 4' - 1. Wegen Q = 0 -siehe Gl (18)- werden im T-S Diagramm dafür keine Flächen ausgewiesen. Der Carnotprozeß bildet im T-S Diagramm ein schmales Rechteck; siehe die Fläche 2' - 3 - 4' - 1 - 2' in Fig. 4, die der Nutzarbeit des Carnotprozesses entspricht.
Befassen wir uns nun mit dem thermischen Wirkungsgrad beider Prozesse. Der thermische Wirkungsgrad ist definiert als das Verhältnis von Nutzarbeit zu zugeführter Energie. Die Nutzarbeit des idealen Stirlingprozesses haben wir mit Gl (25) definiert. Die im idealen Stirlingprozess zugeführte Energie berechnet sich nach Gl (10). So ergibt sich für den Wirkungsgrad des idealen Stirlingprozesses:
(30) 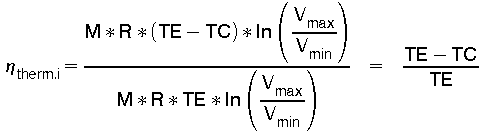
Für den Carnotprozeß haben wir die Nutzarbeit in Gl (28) und Gl (29) definiert. Zugeführt wurde dem Carnotprozeß während der isothermen Expansion vom Volumen Vmin an der Stelle 3 bis zum Volumen V4' an der Stelle 4' die Energie nach Gl (10). Während der adiabatischen Expansion wird zwar auch Nutzarbeit verrichtet; diese zählt, weil sie per Definition ohne äußere Energiezufuhr verrichtet wird -Qadiabat = 0- auch nur als 0-Beitrag zur zugeführten Energie in diesem Prozeß. Somit ergibt sich für den Wirkungsgrad des Carnotprozesses:
(31) 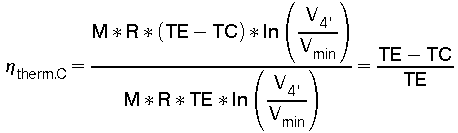
Die Wirkungsgrade dieser beiden idealisierten Wärmekraftprozesse
sind also gleich. Sie hängen nur ab von der zur Verfügung stehenden
Temperaturdifferenz (TE - TC) und der maximalen Temperatur TE des
Prozesses.
Gl (31) ist in der Thermodynamik allgemein als der "Carnot Wirkungsgrad"
hC bekannt. Mit dem Carnot Wirkungsgrad wird
die wichtige Aussage des 2. Hauptsatzes der Thermodynamik untermauert,
daß es keinen Wärmekraftprozeß bzw. keine Maschine geben
kann, die die innere Energie eines Stoffes vollständig in Arbeit umwandeln
kann. Es ist immer nur aus einem Temperaturgefälle heraus Arbeit zu
gewinnen.
Der Carnot Wirkungsgrad ist zudem der maximal mögliche Wirkungsgrad,
der auch nur bei umkehrbaren Zustandsänderungen erreicht werden kann,
wenn also alle irreversiblen Vorgänge -wie z.B. Reibung- ausgeschaltet
sind.
Eine weitere wichtige Aussage des Carnot Wirkungsgrades ist, daß
dieser maximale Wirkungsgrad unabhängig vom verwendeten Arbeitsfluid
ist.
3.1 Der isotherme Stirling Prozeß in einer Maschine mit Kurbeltrieb
Wir stellten im vorigen Kapitel fest, daß ein Wärmekraftprozeß
nach dem idealen Stirlingprozeß einen diskontinuierlichen Bewegungsablauf
haben muß. Die 4 Zustandsänderungen laufen nacheinander ab.
Das kann in einer realen sich schnell drehenden Maschine noch nicht einmal angenähert simuliert
werden. In einem langsam drehenden Stirlingmotor kann durch eine schnelle
mittels Kippschwingung gesteuerte Verdrängerbewegung (schnell im Verhältnis
zur Kurbelwellenumdrehung) der isochore Wärmeübergang einwenig
angenähert werden siehe |6|. Im langsam laufenden Flachplatten-Motor von Ivo Kolin
|14| wird ebenfalls angenähert eine diskontinuirliche Verdrängersteuerung erreicht.
Für einen exakt diskontinuierlichen Bewegungsablauf müßte während der
Expansion der Verdränger (oder bei der a - Typ
Maschine der Kompressionskolben) still stehen; und bei der Kompression müßte wiederum der Verdränger
(bzw bei der a - Typ Maschine müßte jetzt der Expansionskolben) still stehen,
bis jeweils am Ende dieser isothermen Zustandsänderungen der isochore Gaswechsel durch den Regenerator erfolgt.
Der isochore Gaswechsel kann bei der a - Typ Maschine durch gleichzeitige
Bewegung beider Kolben geschehen -ähnlich Fig. 3a. Beim
b - Typ Stirlingmotor müßte
der Arbeitskolben still stehen und nur der Verdrä,nger müßte sich für
den isochoren Gaswechsel bewegen.
An dem folgenden Bild Fig. 3c soll abgeleitet werden, wie man von der diskontinuierlichen Kolbenbewegung des gedachten idealen Stirlingmotors zum kontinuierlich drehenden realen Stirlingmotor mit einem Kurbletrieb gelangt.
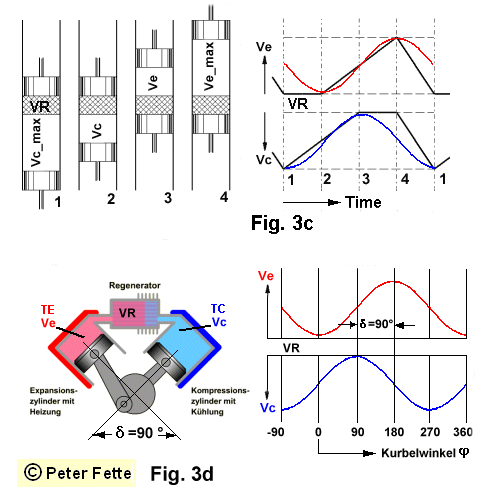
Wir gehen aus von der Darstellung der Volumenänderung des idealen Stirlingprozesses in
Fig. 3b.
Diese Abbildung ist im rechten Bereich der nebenstehenden Abbildung Fig. 3c enthalten.
Betrachten wir die Volumenänderungen separat für den Expansionsraum Ve und den
Kompressionsraum Vc.
Wir haben die diskontinuierliche Kolbenbewegung in Ve in 4 gleiche
Zeitabschnitte eingeteilt und den Beginn dieser Zeitabschnitte bezeichnet mit 1, 2, 3, 4, 1 .
Im 1. Zeitabschnitt ist Ve = 0; dann folgt ein linearer Anstieg des Volumens im 2. und 3.
Zeitabschnitt bis zum Zustandspunkt -4- -dem Endpunkt der isothermen Expansion- auf
Ve_max. Und danach folgt in einem Zeitabschnitt die Reduzierung von Ve_max auf 0.
Wir sind wieder beim Ausgangszustand Ve = 0. Wenn wir jetzt jedem dieser Zeitabschnitte
einen Winkelbereich von 90 ° zuordnen und die lineare diskontinuierliche Kolbenbewegung mit
der sinus-förmigen Kolbenbewegung eines Kurbeltriebes so überlagern, daß die
Extrema Ve = 0 und Ve = Ve_max in etwa den Extrema einer sinus-Kurve entsprechen,
dann gelangen wir von der idealen zur realen sinus-förmigen Kolbenbewegung des
Expansionskolbens eines a- Typ Stirlingmotors; siehe die rote
Sinuskurve in Fig. 3c.
Die gleichen Überlegungen machen wir für die Volumenbewegung im Kompressionsraum
Vc. So gelangen wir zu der realen sinus-förmigen Kolbenbewegung des
Kompressionskolbens siehe die blaue Sinuskurve in Fig. 3c. Eine wichtige weitere Erkenntnis
gewinnen wir, wenn wir den Phasenversatz beider Sinus-Kurven betrachten. Dieser Versatz in
der Kolbenbewegung liegt bei ca. d = 90 Grad Kurbelwinkel.
Der Expansionskolben eilt dem
Kompressionskolben um einen Winkel von d = 90 Grad voraus.
Auf diese Weise wird erreicht,
daß das Arbeitsgas während der Expansion sich überwiegend in den
heißen Regionen des Motors und daß es sich
während der Kompression überwiegend in den kalten Regionen des Motors
aufhält. Die Zustandsänderungen sind beim realen Stirlingmotor nicht mehr scharf
voneinander getrennt, sondern sie überlappen sich.
Fig. 3d zeigt den a- Typ Stirlingmotor. Hier kann der
Phasenversatz von d = 90 ° sehr einfach durch die rechtwinklige
Anordnung der Zylinder in bezug auf
die Kurbelwelle realisiert werden. Beim b- Typ Stirlingmotor
muß der Verdränger dem Arbeitskolben um 90 Grad vorauseilen.
Im Wasserkolben Stirlingmotor |9| oder im Freikolbenmotor (in |7| beschrieben) wird Wasser bzw. eine Metallkolbenmasse so zum Schwingen angeregt, daß eine definierte Phasenverschiebung zu der ebenfalls frei schwingenden Masse des Arbeitskolbens erreicht wird.
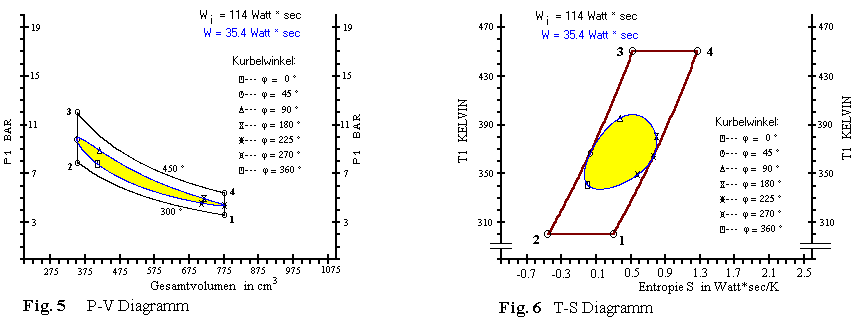
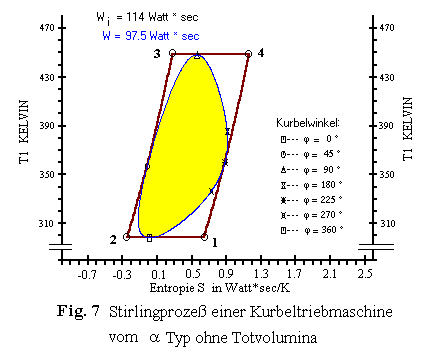
Welche Auswirkung eine sinus-förmige Kolbenbewegung auf den Verlauf des Prozesses
im P-V und im T-S Diagramm hat sehen wir in
Fig. 5 und Fig. 6. In diesen beiden Diagrammen sind die
Zustandsänderungen des idealen Stirlingprozesses eingetragen
mit dem Verlauf 1 - 2 - 3 - 4, wie wir sie schon aus
Fig. 3 und Fig. 4 kennen.
Der Kurvenzug in Fig. 5 und in Fig. 6 gibt den
isothermen Prozeß einer a- Typ
Stirlingmaschine mit einem Regeneratorvolumen und Totvolumina in den Zylindern wieder.
Dieser Kurvenzug umschließt deutlich weniger Fläche (hier gelb
ausgefüllt) als die Fläche "1-2-3-4-1" des idealen Prozesses und bedeutet
damit natürlich auch weniger Nutzarbeit pro Umdrehung -hier 35,4 zu 114 Watt*sec.
Besonders auffällig ist dieser Arbeitsverlust infolge
Überlappung der Zustandsänderungen im Bereich von Vmin bei
der Kurbelwinkelstellung j = 45 ° und im Bereich von
Vmax bei der Kurbelwinkelstellung j = 225 °,
wo beim idealen Prozeß die isochoren Wärmeübergänge stattfinden.
Der ideale Stirlingprozeß bildet eine Art "Rahmen" um den isothermen Prozess
einer Maschine mit Kurbeltrieb.
Rechnet man eine a- Typ Maschine ohne Totvolumina und mit
konstanten Temperaturen (TE im Expansionszylinder, TC im Kompressionszylinder) -so etwas
gibt es in Wirklichkeit natürlich nicht-, dann erkennt man im T-S Diagramm dieses Prozesses
- Fig. 7 - ebenfalls den Arbeitsverlust infolge der sich überlappenden
Zustandsänderungen. Wie in Fig. 5 und Fig. 6
berührt der Kurvenzug die Isochoren bei
Vmin und Vmax; zusätzlich berührt er auch die Isothermen TE und
TC bei der Kurbelwinkelstellung j = 0 ° und bei der
Kurbelwinkelstellung j = 90 °.
Bei dieser theoretischen
Maschine ohne Totvolumina ist bei Kurbelwinkelstellung j = 0 °
der Kolben des Expansionszylinders im oberen Totpunkt; alles Gas befindet sich dann im kalten
Kompressionszylinder und hat die Temperatur TC. Bei j = 90 °
Kurbelwinkelstellung ist der Kolben des Kompressionszylinders im oberen Totpunkt; alles Gas
befindet sich jetzt im heissen Expansionszylinder und hat die Temperatur TE angenommen.
Die Nutzarbeit dieses Prozesses ohne Totvolumina ist mit 97,5 Watt*sec deutlich höher als
die 35,4 Watt*sec der obigen Beispiel Maschine mit Totvolumen und Regeneratorvolumen.
Das Kompressionsverhältnis ist bei dem Prozeß in Fig. 7
Vmax / Vmin = 5,8 während bei dem Prozeß in Fig. 5
das Kompressionsverhältnis Vmax / Vmin = 2,2 ist.
Festzuhalten ist von diesen Überlegungen, daß ein hohes Kompressionsverhältnis
Vmax / Vmin also möglichst wenig Totraum in der Maschine erstrebenswert
ist, um eine hohe Arbeitsausbeute zu bekommen.
Daß jedoch auch noch die Leistung des Erhitzers und die des Kühlers eine wichtige
Rolle dabei spielen, wird später erläutert.
Warum beschäftigen wir uns mit dem idealen Stirlingprozeß, wenn er doch nie zu erreichen ist? Nun einerseits ist es wichtig, die Grenzen eines Wärmekraftprozesses zu kennen, zum andern kann der ideale Prozeß als Bemessungsgrundlage für die Güte eines realen Prozesses dienen. Des weiteren ist es eine allgemein menschliches Bedürfnis, einem Ideal möglichst nahe zu kommen, und dafür müssen wir zunächst einmal dieses Ideal in allen Einzelheiten kennengelernt haben.
Wir müssen leider davon ausgehen, daß es in einem realen Stirlingprozeß keine isothermen Zustandsänderungen gibt. Wie schon vorher erläutert, kann der Wärmeübergang bei einer Temperaturdifferenz von DT = 0 nur äußerst langsam erfolgen.
Man könnte sich jedoch folgende Frage stellen:
Kann für ein konstantes DT > 0
ein Wärmeübergang in der Art erfolgen, daß bei konstanter äußerer
Wärmequellentemperatur TEQ jetzt innerhalb des Stirlingmotors dem Gas auch eine
konstante Temperatur TE aufgeprägt wird? Wenn ja, dann könnte man isotherm weiter rechnen,
wobei dann TE = TEQ - DTE die Temperatur des Gases im
Expansionszylinder ist; bzw auf der kalten Seite im Kompressionszylinder wäre mit
TC = TCQ + DTC zu rechnen.
Wenn dies so wäre, könnte man mit einem relativ einfachen Rechenverfahren den
Wärmekraftprozeß im Stirlingmotor berechnen. Um diese Frage zu beantworten, müssen
wir die benötigte Heizleistung bzw. die Kühlleistung kennen, die der Prozeß
einerseits erfordert, und die andererseits Erhitzer bzw. Kühler in der Lage sein müssen,
bei entsprechendem DT auch zu erbringen. Sind die vom Erhitzer
auf das Gas zu bringende Heizleistung und die im Kühler aus dem Gas abzuziehende
Kühlleistung jeweils konstant,
dann wären auch die Temperaturen TE und TC als konstant zu betrachten.
Dazu folgende Überlegung:
Die für eine isotherme Expansion erforderliche Heizleistung "N" errechnet sich durch Differentiation von Gl (9) nach der Zeit "t"
(32)  für eine
konstante Heizleistung "N"
für eine
konstante Heizleistung "N"
(33) 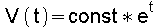
Das bedeutet, nur wenn sich das Volumen (hier bei der Expansion) nach Gl (33) exponentiell ändert, erfolgt bei einer konstanten Heizleistung N und bei konstantem DT > 0 eine isotherme Zustandsänderung. Derartige exponentielle Volumenänderungen kann man sich aber wohl nur in idealisierten Prozessen denken. In realen Stirlingprozessen, in denen die Volumenänderungen sinus-förmig aber nie exponentiell erfolgen, wird also -per Umkehrschluß aus oben Gesagtem- die Energieübertragung auf das Arbeitsfluid während der Expansion bzw Kompression nie mit konstanter Leistung und bei konstanten Temperaturen erfolgen können.
Wichtig: Mit konstanter Heiz- bzw Kühlleistung ist hier nicht die in der Tat konstante Leistung eines Brenners oder der Kühlwasserzufuhr gemeint, sondern die Leistung, die im Expansionsbereich der Maschine auf das Arbeitsfluid übertragen wird, damit dort immer die Temperatur TE herrscht, bzw. die Leistung, die im Kompressionsbereich benötigt wird um das Arbeitsfluid konstant auf TC zu halten.
Ich möchte in diesem Kapitel hauptsächlich den Stirlingmotor behandeln, den ich auf dieser
Homepage vorstelle. Siehe den Bericht dazu. Diese Maschine
benutzt ein bis jetzt noch nicht in Stirlingmotoren angewendetes Verfahren des Wärmetransports
mittels einer Beregnung des Arbeitsgases durch entsprechend heiße bzw. kalte
Arbeitsflüssigkeit. Wie gut dieser Wärmetransport ist, ist noch nicht erforscht. Bisher
durchgeführte Experimente lassen aber auf einen sehr guten
"temperaturgeprägten" Wärmeübergang mit
geringer Grädigkeit DT
schließen. Das würde bedeuten, daß man zwar nicht -wie oben erklärt-
mit einer konstanten Temperatur TE im Expansionszylinder und TC im Kompressionszylinder rechnen
kann, daß aber die Abweichung DT von diesen Temperaturen
gering ist. Was unter "temperaturgeprägten" und "energiegeprägten"
Wärmeübergang zu verstehen ist, wird noch besprochen.
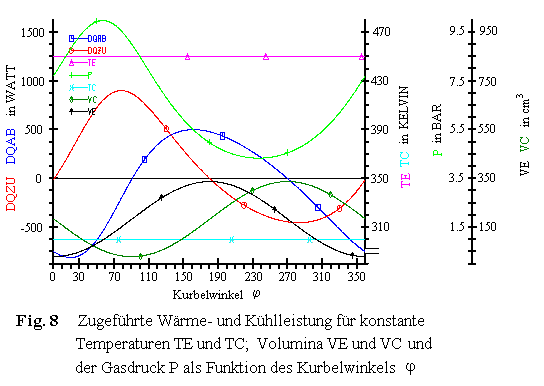 Sehen wir uns Fig. 8 an.
Hier sind für einen isothermen Stirlingprozeß in einer Maschine mit Kurbeltrieb
-also überlappende Zustandsänderungen-
über den Kurbelwinkel j für 1 Umdrehung aufgetragen:
Sehen wir uns Fig. 8 an.
Hier sind für einen isothermen Stirlingprozeß in einer Maschine mit Kurbeltrieb
-also überlappende Zustandsänderungen-
über den Kurbelwinkel j für 1 Umdrehung aufgetragen:
DQZU
die benötigte Wärmezufuhrleistung auf das Arbeitsfluid im Expansionszylinder in Watt,
DQAB
die Kühlleistung im Kompressionszylinder in Watt,
TE und TC die Temperaturen des
Arbeitsfluids in Kelvin,
VE und VC die Volumina in cm3,
P der Druck des Arbeitsfluids in Bar.
Zur Verdeutlichung der Volumenänderungen VE und VC
in Abhängigkeit vom Kurbelwinkel
j ist die Skizze Fig. 16 des
a-Typ Stirlingmotors aus der vorigen Site
"Wie arbeitet der Stirlingmotor" hier wiedergegeben.
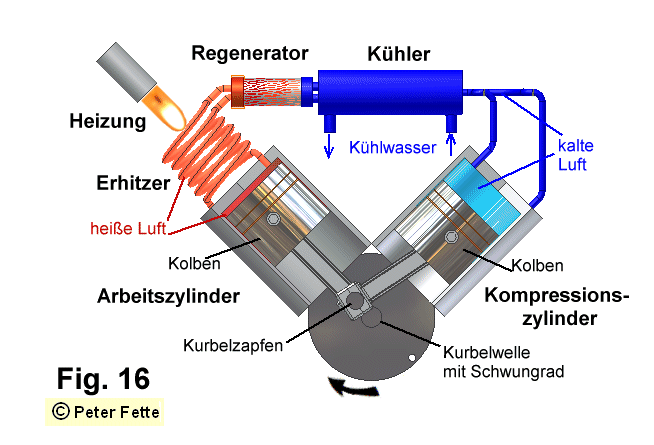
Diese Skizze zeigt in der Kurbelwinkelstellung j = 0 den Kolben
des Expansionszylinders in der oberen Totpunktlage; hier ist VE
ein Minimum; VE besteht hier nur aus dem Totvolumen im
Expansionszylinder. Der Kolben des Kompressionszylinders steht wegen des 90 ° Phasenversatzes
auf 1/2 Hubhöhe, sodaß VC gleich ist 1/2 Hubvolumen +
Totvolumen des Kompressionszylinders. (Möglicherweise finden Sie in anderer Literatur z.B.
auch in |7| den Winkel j = 0 bezogen auf die Kolbenstellung
des Kompressionszylinders in der unteren Totpunktlage.) Hier wollen wir uns aber auf die in
Fig. 8 und Fig. 16 definierte Ausgangsstellung des Kurbelwinkels
j = 0 beziehen.
Betrachten wir in Fig. 8 den Verlauf der zugeführten Wämeleistung DQZU , so erkennen wir, daß ab 180° DQZU negativ werden muß um die konstante Temperatur TE halten zu können. Negative "Heizleistung" bedeutet aber Kühlung ! Warum dies?? Nun, es ist hier ein isothermer Stirlingprozeß für eine Maschine mit Kurbeltrieb gerechnet worden. Während der Expansion in VE von Kurbelwinkelstellung j = 0 bis 180 ° muß gem. Gl (8) Wärme zugeführt werden. Ab j = 180 ° verkleinert sich das Expansionsvolumen VE wieder, es beginnt jetzt im Expansionszylinder eine Kompression. Selbst wenn jetzt keine Wärme mehr zugeführt wird, würde die Temperatur TE ansteigen entsprechend einer adiabatischen Kompression gem. Gl (19). Errechnen könnte man diese Temperatursteigerung bei adiabatischer Kompression mit Gl (21) wobei hier für Vmin das jeweils erreichte Volumen einzusetzen ist. Wir haben aber einen isothermen Prozeß gerechnet! In diesem Prozeß darf TE sich nicht ändern, darum muß ab 180 ° Kurbelwinkel bei der jetzt im Expansionszylinder einsetzenden Kompression gekühlt werden: DQZU wird negativ! Ebenso nur mit umgekehrten Vorzeichen verhält es sich im Kompressionszylinder, wenn hier für TC isotherm gerechnet wird. In dem Kurbelwinkelbereich (90 bis 270 °), in dem sich das Volumen VC im Kompressionszylinder wieder vergrößert, wird DQAB positiv, d.h. hier muß statt Kühlung jetzt Wärme zugeführt werden, damit TC konstant bleibt !!
Was bedeuten diese Ausführungen ??
In einer realen Maschine wird mit Sicherheit keine
wechselnde Erhitzung DQZU und wechselnde Kühlung
DQAB in den Zylindern stattfinden können, damit optimale
isotherme Verhältnisse erreicht werden. Die Erhitzerenergie wird konstant zugeführt und
ebenso wird im Kühler der Maschine ein konstanter Kühlwasserstrom fließen.
Die durch den Kurbeltrieb erzwungenen Volumenänderungen bewirken Druckänderungen, die,
wie wir oben gelernt haben, Temperaturänderungen aufgrund adiabatischer Zustandsänderungen
zur Folge haben, wenn das System isoliert wäre -also ohne Erhitzung und Kühlung; siehe
auch Fig. 2d.
Jedoch bei konstanter Energiezufuhr im Erhitzer bzw. im Expansionszylinder und bei konstanter
Kühlung im Kühler bzw. im Kompressionszylinder haben die durch den Kurbeltrieb
erzwungenen Volumen- und Druckänderungen jetzt polytrope Zustandsänderungen zur Folge;
siehe auch Fig. 2e. Rein polytrope Zustandsänderungen sind es jedoch
auch nicht mit denen man rechnen kann. Wir müssen die Gaswechselvorgänge von heiß
nach kalt und umgekehrt und den damit verbundenen Energieaustausch
auch noch mit berücksichtigen, um die Ursache für die wechselnden Temperaturen in der
Maschine zu erklären. Dies ist rechnerisch eine hoch komplizierte Angelegenheit. Geschlossene
Lösungen, wie sie z.B. bereits vor über 130 Jahren G.Schmidt |8|
genial für den isothermen Prozeß aufstellen konnte, sind nicht möglich. Erst moderne
Computer gestatten Näherungsrechnungen für diese Problematik. In |7|
und in |13| werden Rechenverfahren vorgestellt. Man teilt die Volumina einer
Maschine in viele kleine Abschnitte auf, in denen man zunächst "konstante"
Temperaturen annimmt. In mehrfachen Iterationen bei möglichst kleiner Rechenschrittweite
ermittelt man dann die Massenströme, vergleicht sie mit dem vorherigen Rechenvorgang, wendet
Korrekturen an, und wiederholt die Rechnung bis ein nach gewissen Kriterien stabiler Zustand
errechnet worden ist.
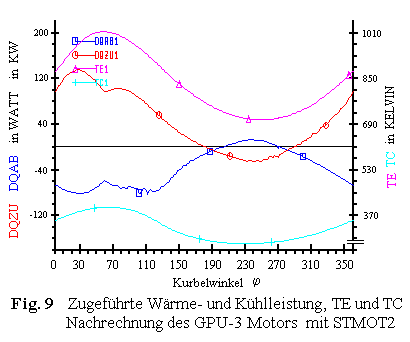 In einem realen Stirlingprozeß sehen die Kurven für DQZU
und DQAB demzufolge anders aus. Siehe
Fig. 9. Hier ist mit dem Programm
STMOT2 der in |7| detailliert beschriebene
Stirlingmotor GPU-3 nachgerechnet worden. Eingabe für STMOT2
war hierbei das Temperaturprofil, welches mit dem in |7| angegebenen FORTRAN
Programm errechnet wurde.
In einem realen Stirlingprozeß sehen die Kurven für DQZU
und DQAB demzufolge anders aus. Siehe
Fig. 9. Hier ist mit dem Programm
STMOT2 der in |7| detailliert beschriebene
Stirlingmotor GPU-3 nachgerechnet worden. Eingabe für STMOT2
war hierbei das Temperaturprofil, welches mit dem in |7| angegebenen FORTRAN
Programm errechnet wurde.
Sehen wir uns den Verlauf von DQZU und
DQAB hier an an, so fällt auf, daß
DQZU hier kaum negativ wird und DQAB
wird kaum positiv. Die Temperaturen TE und TC
sind starken Schwankungen unterworfen. Hier in der realen Maschine finden während der
Kompression und Expansion überlappende Zustandsänderungen statt. Man könnte die
Temperaturen TE und TC
berechnen aus polytropen Zustandsänderungen mit sich ändernden Polytropenexponenten.
Natürlich fragt man sich, warum wird DQZU
hier -wenn auch gering- negativ und warum wird DQAB geringfügig
positiv ? Ich möchte diese Frage
so beantworten: STMOT2 hat diese Energiebeträge gerechnet für ein Temperaturprofil, das
mit dem FORTRAN Programm aus |7| errechnet wurde. In STMOT2 kann die Konfiguration
der GPU-3 Maschine nicht eingegeben werden, da STMOT2 keinen separaten Erhitzer und Kühler
kennt und auch einen Druckverlust im Regenerator nicht berücksichtigt. Insofern sind die hier
berechneten Werte ungenau. Das FORTRAN Programm in |7| kann wiederum nicht die
Werte für DQZU und DQAB ausgeben.
Die zu diesem Prozeß gehörenden P-V und T-S Diagramme gibt Fig. 10
wieder. Zum P-V Diagramm sei hier nocheinmal darauf hingewiesen, daß der Prozeß mit
STMOT2 ohne Druckverlust im Regenerator gerechnet wurde. Dies entspricht nicht der Realität
dieser mit 2500 U/min sehr schnell laufenden Maschine GPU-3. Eigentlich müssen wegen der
unterschiedlichen Druckverhätnisse im Expansionszylinder und Kompressionszylinder 2 getrennte
P-V Diagramme erstellt werden.
(Das Programm STMOT2 ist hauptsächlich zur Berechnung des
langsam drehenden 2 mal doppelt wirkenden Niedertemperatur Stirlingmotors entwickelt.)
Dennoch vermittelt das P-V Diagramm in Fig. 10 einen Eindruck, wie der
Arbeitsprozeß einer realen Maschine sich von dem des idealen Stirlingprozesses unterscheidet.
Das gleiche gilt für das T-S Diagramm in Fig. 10. In diesem T-S Diagramm
sind auch deutlich die Krümmungen der Isochoren Vmin (Linienzug 2-3) und
Vmax (Linienzug 4-1) des mit eingezeichneten idealen Stirlingprozesses zu erkennen.
In den T-S Diagrammen Fig. 6 und Fig. 7 sind die Isochoren
wegen des geringeren Temperaturbereichs Tmin bis Tmax kaum als gekrümmte
Linien, eher als Geraden zu sehen.
Man beachte auch die ganz andere Form der gelb ausgefüllten Flächen, die ja die
Nutzarbeit in diesen T-S Diagrammen darstellen.
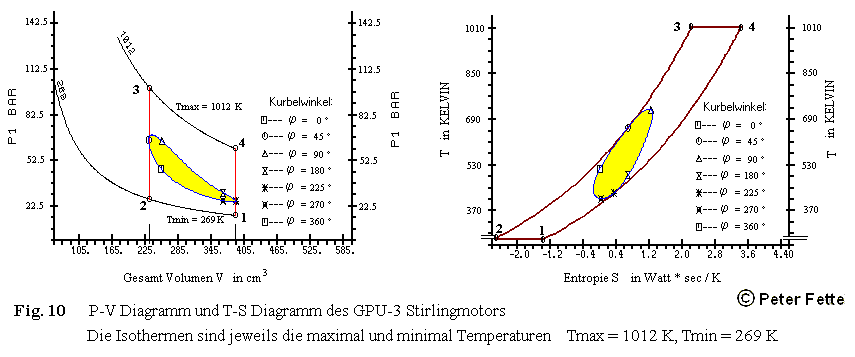
Das Verhältnis der Nutzarbeit des realen Prozesses -die gelb ausgefüllte Fläche- zur Nutzarbeit des idealen Stirlingprozesses -das ist die durch die Linien 1-2-3-4-1 eingeschlossene Fläche- sei "Ausnutzungsgrad" e genannt. Dieser Ausnutzungsgrad e stellt die Güte des Prozesses dar. Er ist um so höher je weniger Totraum in der Maschine ist; bzw. er ist um so höher je höher auch das Kompressionsverhältnis ist. Für eine Maschine mit Kurbeltrieb und gleichen Durchmessern von Expansions- und Kompressionszylinder ist der theoretisch maximale Ausnutzungsgrad ei = 65 % erreicht bei einem Kompressionsverhältnis von Vmax/Vmin = 5.83 entsprechend dem im T-S Diagramm Fig. 7 dargestellten isothermen Prozeß ohne jeglichen Totraum sowohl in Expansions- und Kompressionszylinder als auch im Regenerator.
Immer, wenn die Luft vom kalten in den heißen Bereich gedrückt wird, sei es durch die
Bewegung des Verdrängers in den b-Maschinen
oder
durch die Kolbenbewegung in den a-Maschinen, muß die Luft zunächst
einmal wieder aufgeheizt werden, bevor sie durch weitere Wärmezufuhr Arbeit verrichten kann.
Und umgekehrt, wenn die Luft vom heißen in den kalten Bereich verschoben wird,
sollte sie erst schon einmal vorgekühlt werden, bevor bei weiterer Kühlung die
Kompression erfolgen kann.
Wenn man nun diese Energie, die die Luft auf dem einen Weg mal abgeben muß, und die ihr auf
dem Rückweg wieder hinzugefügt werden muß,
zwischenspeichern könnte, und im richtigen Moment wieder laden könnte, dann
wäre viel gewonnen.
Diese Energiezwischenspeicherung ist die Aufgabe
des Regenerators. Wie sein Name schon sagt, soll er etwas regenerieren. Und zwar soll er den Zustand
"heiß" wieder regenerieren, wenn die Luft vom kalten in den heißen Bereich zurück
kommt, und umgekehrt soll er den Zustand "kalt" regenerieren, wenn die Luft vom heißen
in den kalten Bereich gedrückt wird.
Bei den a-Maschinen können wir uns den Regenerator als ein
Stück Rohr zwischen Kompressions- und Arbeitszylinder vorstellen, in dem ein dichtgepacktes
Drahtgeflecht sitzt.

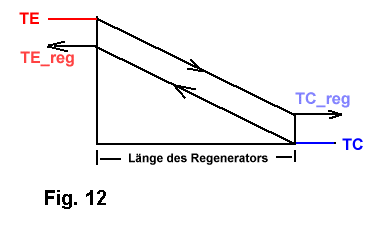
Die Wirkung ist folgende und soll durch die rote über orange bis hin zur und blauen
Färbung in Fig. 11 verdeutlicht werden:
Da die Gasmasse, die durch den Regenerator strömt, entsprechend der Bewegung beider Kolben
eine Funktion der Zeit und des Druckes ist, sind die Temperaturen, mit denen das Gas jeweils den Regenerator
verläßt nicht so einfach zu berechnen. Wir gewinnen aber einen Überblick, wenn wir folgende
Vereinfachungen für den Regenerator treffen:
(34) 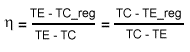
Fragen, Anregungen ? Bitte
|1| R.W. Pohl: Mechanik, Akustik und Wärmelehre, Springer Verlag Berlin, Göttingen, Heidelberg 1964. Library of Congress Catalog Card Number 64-25424.
|2| H. Hausen: Thermodynamik, Scriptum der Vorlesungen: Technische Wärmelehre I
|3| R.J.Meijers: Der Philips Stirlingmotor, Motoren Technische Zeitschrift MTZ 29(1968)/7, DK 621.41/43 (492) Philips
|4| P.Fette: STMOT2 Ein Computerprogram zur Berechnung des Wärmekraftprozesses und der Dynamik von Alpha-Typ Stirlingmotoren
|5| P. Fette Grundlagen für die Berechnung des Wärmekraftprozesses und der Dynamik von a -Typ Stirlingmotoren mit dem Programm STMOT2
|6| James C. Senft, Ringbom Stirling Engines Oxford University Press 1993; ISBN 0-19- 507798-9
|7| Israel Urieli, David M. Berchowitz, Stirling Cycle Engine Analysis Adam Hilger Ltd, Bristol 1984; ISBN 0-85274-435-8
|8| Gustav Schmidt, Theorie der Lehmann'schen calorischen Maschine Zeitschrift des Vereins deutscher Ingenieure 1871 Band XV Heft 1 Januarheft Seiten 1-12 dazu Tafel III und Heft 2 Februarheft Seiten 97 bis 112
|9| C. D. West, Liquid Piston Stirling Engines , Van Nostrand Reinold Company New York 1983 ISBN 0-442-29237-6
|10| G. Walker, Stirling Engines, Clarendon Press Oxford 1980
|11| R.J.Meijers. Der Philips Stirlingmotor, Motoren Technische Zeitschrift MTZ 29(1968)/7, DK 621.41/43 (492) Philips
|12| Manfred Künzel, Stirlingmotor der Zukunft, Fortschr. Berichte, VDI Reihe 6 Nr. 193. Düsseldorf: VDI-Verlag 1986. ISBN 3-18-149306-6
|13| Ghassan Hadj-Obid, .. Auslegung und Optimierung eines Sonnen-Stirlingmotors, Fortschr. Berichte, VDI Reihe 6 Nr. 166. Düsseldorf: VDI-Verlag 1985. ISBN 3-18-146606-9
|14| Ivo Kolin; STIRLING MOTOR history- theory- practice; Dubrownik 1991